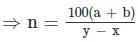CDS I - Mathematics Previous Year Question Paper 2016 - CDS MCQ
30 Questions MCQ Test - CDS I - Mathematics Previous Year Question Paper 2016
If λ is an integer and α, β are the roots of 4x2 – 16x + λ/4 = 0 such that 1 < α < 2 and 2 < β < 3, then how many values can λ take?
If x2 = y + z, y2 = z + x and z2 = x + y, then what is the value of 
What would be the maximum value of Q in the equation 5P9 + 3R7 + 2Q8 = 1114?
A is a set of positive integers such that when divided by 2, 3, 4, 5 and 6 leaves the reminder 1, 2, 3, 4 and 5 respectively. How many integers between 0 and 100 belong to the set A?
In an examination, a student was asked to divide a certain number by 8. By mistake he multiplied it by 8 and got the answer 2016 more than the correct answer. What was the number?
In the quadratic equation x2 + ax + b = 0, a and b can take any value from the set {1, 2, 3, 4}. How many pairs of values of a and b are possible in order that the quadratic equation has real roots?
The sum of squares of two positive integers is 208. If the square of the larger number is 18 times the smaller number, then what is the difference of the larger and smaller numbers.
Let A = {7, 8, 9, 10, 11, 12} and B = {7, 10, 14, 15}. What is the number of elements in (A – B) and (B – A) respectively?
A boy saves Rs. 4.65 daily. What is the least number of days in which he will be able to save an exact number of rupees?
Two men, A and B run a 4 km race on a course 0.25 km round. If their speeds are in the ratio 5 : 4, how often does the winner pass the other?
Which one of the following rational numbers has non-terminating and repeating decimal expression?
If α and β are the two zeros of the polynomial 25x2 – 15x + 2, then what is a quadratic polynomial whose zeros are (2α)-1 and (2β)-1 ?
What is the remainder when 2100 is divided by 101?
In an office, one-third of the workers are women, half of the women are married, and one-third of the married women have children. If three-fourth of the men are married and one-third of the married men have children, then what is the ratio of married women to married men?
A can do 50% more work than B in same time. B alone can do a piece of work in 30 hours. B starts working and had already worked for 12 hours when A joins him. How many hours should B and A work together to complete the remaining work?
When the speed of a train is increased by 20%, it takes 20 minutes less to cover the same distance. What is the time taken to cover the same distance with the original speed?
The cost of 2.5 kg rice is Rs. 125. The cost of 9 kg rice is equal to that of 4 kg pulses. The cost of 14 kg pulses is equal to that of 1.5 kg tea. The cost of 2 kg tea is equal to that of 5 kg nuts. What is the cost of 11 kg nuts?
There are 12 friends A, B, C, D, E, F, G, H, I, J, K and L who invested money in some business in the ratio of 1 : 2 : 3 : 4 : 5 : 6 : 7 : 8 : 9 : 10 : 11 : 12 and the duration for which they invested the money is in the ratio of 12 : 11 : 10 : 9 : 8 : 7 : 6 : 5 : 4 : 3 : 2 : 1 respectively. Who will get the maximum benefit at the end of the year?
If p and q are the roots of x2 + px + q = 0, then which of the following is correct?
Which of the following is correct in respect to number 1729?
A shopkeeper increases the cost price of an item by 20% and offers a discount of 10% on this marked price. What is his percentage gain?
There are two numbers p and q such that their HCF is 1. Which of the following statements are correct?
1. Both p and q may be prime.
2. One number may be prime and the other composite.
3. Both the numbers may be composite.
Select the correct answer using the code given below:
A person can row downstream 20 km in 2 hours and upstream 4 km in 2 hours. What is the speed of the current?
Consider the following statements in respect of positive odd integers x and y:
1. x2 + y2 is even integer.
2. x2 + y2 is divisible by 4.
Q. Which of the above statements is/are correct?
What are the roots of the equation 2x + 2 × 27x/x - 1 = 9?
2122 + 462 + 842 + 464 + 2130 is divisible by which one of the following integers?
A candidate scoring x% marks in an examination fails by ‘a’ marks, while another candidate who scores y% marks gets ‘b’ marks more than the minimum pass marks. What is the maximum mark for the examination?