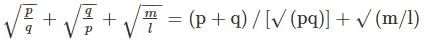CDS II - Mathematics Previous Year Question Paper 2016 - CDS MCQ
30 Questions MCQ Test - CDS II - Mathematics Previous Year Question Paper 2016
If the roots of the equation lx2 + mx + m = 0 are in the ratio p ∶ q, then 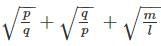 is equal to
is equal to
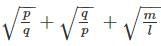 is equal to
is equal toIf √(3x2 - 7x - 30) - √(2x2 - 7x - 5) = x - 5 has α and β as its roots, then the value of αβ is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If p/x + q/y = m and q/x + p/y = n, then what is x/y equal to?
If a2 - by - cz = 0, ax - b2 + cz = 0 and ax+ by - c2 = 0, then what is the value of x/(a + x) + y/(b + y) + z/(c + z) will be
If the equations x2 - px + q = 0 and x2 + qx - p = 0 have a common root, then which one of the following is correct?
If x = 21/3 + 2-1/3, then the value of 2x3 - 6x - 5 is equal to
The sum and difference of two expressions are 5x2 - x - 4 and x2 + 9x - 10 respectively. The HCF of the two expressions will be
If (s - a) + (s - b) + (s - c) = s, then the value of [(s - a)2 + (s - b)2 + (s - c)2 + s2] / (a2 + b2 + c2) will be
If the polynomial x6 + px5 + qx4 - x2 - x - 3 is divisible by (x4 - 1), then the value of p2 + q2 is
Let p and q be non-zero integers. Consider the polynomial A(x) = x2 + px + q. It is given that (x - m) and (x - km) are simple factors of A(x), where m is a non-zero integer and k is positive integer, k ≥ 2. Which one of the following is correct?
Let m be a non-zero integer and n be a positive integer. Let R be the remainder obtained on dividing the polynomial xn + mn by (x – m). Then
If 4x2y = 128 and 33x 32y – 9xy = 0, then the value of x + y can be equal to
If the linear factors of ax2 - (a2 + 1) x + a are p and q, then p + q is equal to
If x = [√(a + 2b) + √(a - 2b)]/[√(a + 2b) - √(a - 2b)], then bx2 - ax + b is equal to (given that b ≠ 0)
If a3 = 117 + b3 and a = 3 + b, then the value of a + b is (given that a > 0 and b > 0)
If the sum of the roots of ax2 + bx + c = 0 is equal to the sum of the squares of their reciprocals, then which one of the following relation is correct?
Consider the following statements in respect of the expression Sn = n(n + 1)/2
where n is an integer
I. There are exactly two values of n for which Sn = 861
II. Sn = S-(n + 1) and hence for any integer m, we have two values of n for which Sn = m
Q. Which of the above are not perfect squares?
Consider the following statements in respect of two different non-zero integers p and q:
I. For (p + q) to be less than (p - q), q must be negative
II. For (p + q) to be greater than (p - q), both p and q must be positive
Q. Which of the above statements is/are correct?
If a/b = b/c = c/d, then which of the following is/are correct?
I. (b3 + c3 + d3) / (a3 + b3 + c3) = d/a
II. (a2 + b2 + c2) / (b2 + c2 + d2) = a/d
Select the correct answer using the code given below.
Let a two digit number be k times the sum of its digits. If the number formed by interchanging the digits is m times the sum of the digits, then the value of m is
A man walking at 5 km/hr noticed that a 225 m long train coming in the opposite direction crossed him in 9 seconds. The speed of the train is
(sin 35°/cos 55°)2 - (cos 55°/sin 35°)2 + 2sin 30° is equal to
A cyclist moves non-stop from A to B, a distance of 14 km, at a certain average speed. If his average speed reduces by 1 km per hour, he takes 20 minutes more to cover the same distance. The original average speed of the cyclist is
If a sum of money at a certain rate of simple interest per year doubles in 5 years and at a different rate of simple interest per year becomes three times in 12 years, then the difference in the two rates of simple interest per year is
If each interior angle of a regular polygon is 140°, then the number of vertices of the polygon is equal to
Let the triangles ABC and DEF be such that ∠ABC = ∠DEF, ∠ACB = ∠DFE and ∠BAC = ∠EDF. Let L be the midpoint of BC and M be the point of EF. Consider the following statements:
Statement I: Triangle ABL and DEM are similar
Statement II: Triangle ALC is congruent to triangle DMF even if AC ≠ DF
Q. Which one of the following is correct in respect of the above statements?
The number of rounds that a wheel of diameter 7/11 meter will make in traversing 4 km will be
The base of an isosceles triangle is 300 units and each of its equal sides 170 units. Then area of the triangle is
Four equal discs are placed such that each one touches two others. If the area of empty space enclosed by them is 150/847 square centimeter, then the radius of each disc is equal to