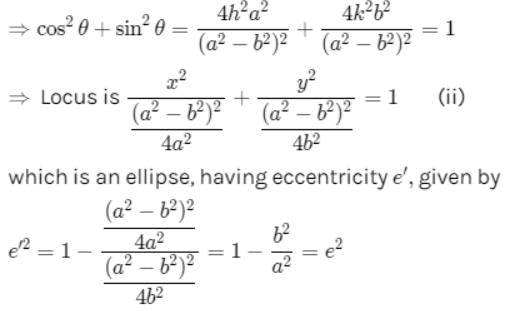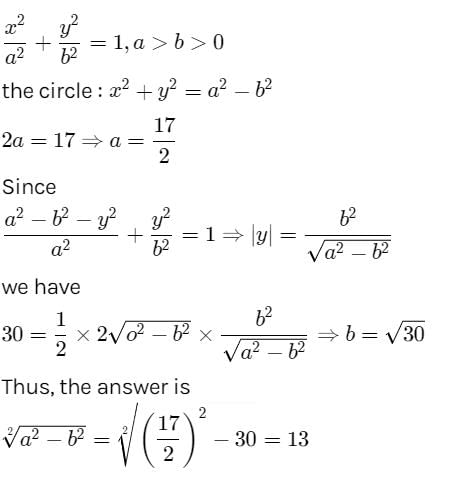Test: Ellipse- 5 - JEE MCQ
23 Questions MCQ Test - Test: Ellipse- 5
x – 2y + 4 = 0 is a common tangent to y2 = 4x & 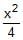 +
+ 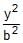 = 1. Then the value of b and the other common tangent are given by
= 1. Then the value of b and the other common tangent are given by
The area of the rectangle formed by the perpendiculars from the centre of the standard ellipse to the tangent and normal at its point whose eccentric angle is π/4 is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
An ellipse is such that the length of the latus rectum is equal to the sum of the lengths of its semi principal axes. Then
The line, lx + my + n = 0 will cut the ellipse +
= 1 in points whose eccentric angles differ by p/2 if
The normal at a variable point P on an ellipse +
= 1 of eccentricity e meets the axes of the ellipse in Q and R then the locus of the mid-point of QR is a conic with an eccentricity e' such that
The length of the normal (terminated by the major axis) at a point of the ellipse +
= 1 is where r and r1 are the focal distance of the point.
The tangent at any point P on a standard ellipse with foci as S & S¢ meets the tangents at the vertcies A & A¢ in the points V & V¢, then
A circle has the same centre as an ellipse & passes through the foci F1 & F2 of the ellipse, such that the two curves intersect in 4 points. Let `P' be any one of their point of intersection. If the major axis of the ellipse is 17 & the area of the triangle PF1F2 is 30, then the distance between the foci is less than
Point `O' is the centre of the ellipse with major axis AB and minor axis CD. Point F is one focus of the ellipse. If OF = 6 and the diameter of the inscribed circle of triangle OCF is 2, then the product (AB)(CD) is less than
If P is a point of the ellipse +
=1, whose focii are S and S'. Let ∠PSS' = a and ∠PS'S = b, then
If the chord through the points whose eccentric angles are q & f on the ellipse, +
= 1 passes through the focus, then the value of tan (q/2) tan (f/2) is
Consider an ellipse +
= 1 with centre C and a1 point P on it with eccentric angle
. Normal drawn at P intersects the major and minor axes in A and B respectively. N1 and N2 are the feet of the perpendiculars from the foci S1and S2 respectively on the tangent at P and N is the foot of the perpendicular from the centre of the ellipse on the normal at P. Tangent at P intersects the axis of x at T. Match the entries of Column-I with the entries of Column-II.
Column-I Column-II
(A) (CA)(CT) is equal to (P) 9
(B) (PN)(PB) is equal to (Q) 16
(C) (S1N1)(S2N2 ) is equal to (R) 17
(D) (S1P)(S2P) is equal to (S) 25
Find the equations of the lines with equal intercepts on the axes & which touch the ellipse +
= 1.
Suppose x and y are real numbers and that
x2 + 9y2 – 4x + 6y + 4 = 0 then find the maximum value of (4x – 9y).
A tangent having slope _ to the ellipse
+
= 1, intersects the axis of x & y in points A & B respectively. If O is the origin, find the area of triangle OAB.
`O' is the origin & also the centre of two concentric circles having radii of the inner & the outer circle as `a' & `b' respectively. A line OPQ is drawn to cut the inner circle in P & the outer circle in Q. PR is drawn parallel to the y-axis & QR is drawn parallel to the x-axis. Prove that the locus of R is an ellipse touching the two circles. If the focii of this ellipse lie on the inner circle, find the ratio of inner : outer radii & find also the eccentricity of the ellipse.
Common tangents are drawn to the parabola
y2 = 4x & the ellipse 3x2 + 8y2 = 48 touching the parabola at A & B and the ellipse at C & D. Find the area of the quadrilateral.
An ellipse has foci at F1(9, 20) and F2(49, 55) in the xy-plane and is tangent to the x-axis. Find the length of its major axis.
Given the equation of the ellipse +
=1, a parabola is such that its vertex is the lowest point of the ellipse and it passes through the ends of the minor axis of the ellipse. The equation of the parabola is in the form 16y = a(x – h)2 – k. Determine the value of (a + h + k).
A tangent to the ellipse +
= 1 touches at the point P on it in the first quadrant & meets the coordinate axes in A & B respectively. If P divides AB in the ratio 3 : 1 reckoning from the x-axis find the equation of the tangent.
Rectangle ABCD has area 200. An ellipse with area 200p passes through A and C and has foci at B and D. Find the perimeter of the rectangle.
A ray emanating from the point (– 4, 0) is incident on the ellipse 9x2 + 25y2 = 225 at the point P with abscissa 3. Find the equation of the reflected ray after first reflection.
Variable pairs of chords at right angles and drawn through any point P (with eccentric angle p/4) on the ellipse + y2 = 1, to meet the ellipse at two points say A and B. If the line joining A and B passes through a fixed point Q(a, b) such that a2 + b2 has the value equal to
, where m, n are relatively prime positive integers, find (m + n).