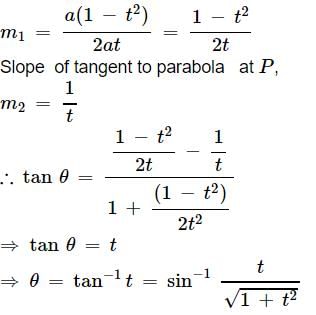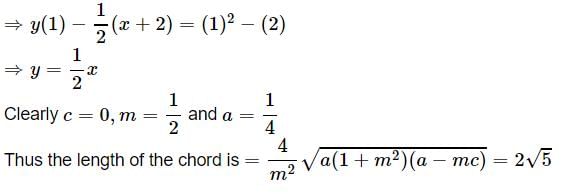All Courses
Get the App Signup / Login
Sign in Open App
JEE Exam  >  JEE Tests  >  Test: Parabola- 4 - JEE MCQ

Test: Parabola- 4 - JEE MCQ


Test Description

15 Questions MCQ Test - Test: Parabola- 4

Test: Parabola- 4 for JEE 2024 is part of JEE preparation. The Test: Parabola- 4 questions and answers have been prepared according to the JEE exam syllabus.The Test: Parabola- 4 MCQs are made for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Parabola- 4 below.
Solutions of Test: Parabola- 4 questions in English are available as part of our course for JEE & Test: Parabola- 4 solutions in Hindi for JEE course. Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt Test: Parabola- 4 | 15 questions in 30 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
Test: Parabola- 4 - Question 1
Save

The straight line joining any point P on the parabola y2 = 4ax to the vertex and perpendicular from the focus to the tangent at P, intersect at R, then the equation of the locus of R is

Detailed Solution for Test: Parabola- 4 - Question 1

Given the equation of parabola is
y2 = 4ax
Let P(at2, 2at) be any point on the parabola.
Equation of tangent at point P is ty = x + at2  where slope of the tangent is 1/t.  
Equation of line perpendicular to the tangent passes through (a,0) is given as
∴ y−0 = −t(x−a) 
or y = t(a−x)                        .....(i)
Equation of OP is given by
y−0 = 2/t(x−0) = 0 
⇒ y = 2x/t                            .....(ii)
Eliminating 't' from equations (i) and (ii), we get
y2 = 2x(a−x)
or  2x2 + y2 − 2ax = 0

Test: Parabola- 4 - Question 2
Save

PQ is a normal chord of the parabola y2 = 4ax at P, A being the vertex of the parabola. Through P a line is drawn parallel to AQ meeting the x-axis in R. Then the length of AR is

Detailed Solution for Test: Parabola- 4 - Question 2

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Parabola- 4 - Question 3
Save

If the tangents and normals at the extremities of a focal chord of a parabola intersect at (x1, y1) and (x2, y2) respectively, then

Detailed Solution for Test: Parabola- 4 - Question 3

If the parabola is Y2= 4ax
 
take the focal chord which is easy for calculation e.x. LR (latus rectum)
then coordinates of extremities would be (a,2a) and (a,-2a)
 
equation of tangent of parabola at (a,2a) :
T=0 : 2ay = 2a(x+a)
y = x+a................................. (1)
equation of tangent of parabola at (a,-2a) :
T=0 -2ay = 2a (x+a)
y = -x-a .........................(2)
point of intersection of both tangents is (X1, Y1)
after solving eq1 and eq2 X1 = -a and Y1 = 0
so ( -a, 0)
eqn of normal of parabola at (a, 2a)
y = -x +3a ...............................(3)
 
eqn of normal of parabola at (a, -2a)
y = x -3a..............................(4)
so point of intersection of normal's : (X2, Y2)
after solving eq3 and eq4 X2= 3a and Y2 = 0
so we conclude... for y2= 4ax
Y1= Y2

Test: Parabola- 4 - Question 4
Save

From point P two tangents are drawn from it to the parabola y2 = 4x such that the slope of one tangent is three times the slope of the other. The locus of P is
Test: Parabola- 4 - Question 5
Save

The equation of a straight line passing through the point (3, 6) and cutting the curve y = √x orthogonally is
Detailed Solution for Test: Parabola- 4 - Question 5

The curve y=(x)1/2 is the part of curve y2=x
Equation of normal at P(t2/4, t/2) is
y+tx=t/2+t3/4..... (1)
The equation will pass through (3,6)
6+3t=t/2+t3/4
t3−10t−24=0
Solving, we get t=4
So equation of line which is orthogonal and passes through (3,6) is
y+4x=18
4x+y-18 = 0

Test: Parabola- 4 - Question 6
Save

The tangent and normal at P (t), for all real positive t, to the parabola y2 = 4ax meet the axis of the parabola in T and G respectively, then the angle at which the tangent at P to the parabola is inclined to the tangent at P to the circle through the points P, T and G is
Detailed Solution for Test: Parabola- 4 - Question 6

Equation of tangent and normal at P(at2,2at) on y2=4ax are
ty=x+at2.....(1)
y+tx=2at+at3...(2)
So, T(−at2,0) & G(2a+at2,0) 
Equation of circle passing through P,T and G is
(x+at2)(x−(2a+at2))+(y−0)(y−0)=0
x2+y2−2ax−at2(2a+at2)=0
Equation of tangent on the above circle at P(at2,2at) is at2x+2aty−a(x+at2)−at2(2a+at2)=0
Slope of line which is tangent to circle at P

Test: Parabola- 4 - Question 7
Save

AB, AC are tangents to a parabola y2 = 4ax. p1 p2 and p3 are the lengths of the perpendiculars from A, B and C respectively on any tangent to the curve, then p2, p1, p3 are in
Detailed Solution for Test: Parabola- 4 - Question 7

Test: Parabola- 4 - Question 8
Save

Through the vertex O of the parabola, y2 = 4ax two chords OP and OQ are drawn and the circles on OP and OQ as diameter intersect in R. If q1, q2 and f are the angles made with the axis by the tangent at P and Q on the parabola and by OR then the value of cotq1 + cotq2 equals
*Multiple options can be correct
Test: Parabola- 4 - Question 9
Save

Let A be the vertex and L the length of the latus rectum of parabola, y2 – 2y – 4x – 7 = 0. The equation of the parabola with point A as vertex, 2L as the length of the latus rectum and the axis at right angles to that of the given curve is
*Multiple options can be correct
Test: Parabola- 4 - Question 10
Save

Tangent to the parabola y2 = 4ax at point P meets the tangents at vertex A at point B and the axis of parabola at T, Q is any point on this tangent and N as the foot of perpendicular from Q on SP, where S is focus, M is the foot of perpendicular from Q on the directrix then
*Multiple options can be correct
Test: Parabola- 4 - Question 11
Save

The parametric coordinates of any point on the parabola y2 = 4ax can be
Detailed Solution for Test: Parabola- 4 - Question 11

Parametric coordinates of the parabola y2 = 4ax are (at2, 2at).

*Multiple options can be correct
Test: Parabola- 4 - Question 12
Save

The length of the chord of the parabola y2 = x which is bisected at the point (2, 1) is less than
Detailed Solution for Test: Parabola- 4 - Question 12

Equation of chord to the given parabola with given mid point (2,1) is given by, 
T = S1

*Multiple options can be correct
Test: Parabola- 4 - Question 13
Save

The locus of the mid point of the focal radii of a variable point moving on the parabola, y2 = 4ax is a parabola whose
*Multiple options can be correct
Test: Parabola- 4 - Question 14
Save

A variable circle is described to passes through the point (1, 0) and tangent to the curve y = tan(tan-1x). The locus of the centre of the circle is a parabola whose
*Multiple options can be correct
Test: Parabola- 4 - Question 15
Save

Two parabolas have the same focus. If their directrices are the x-axis & the y-axis respectively, then the slope of their common chord is
Information about Test: Parabola- 4 Page
In this test you can find the Exam questions for Test: Parabola- 4 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Parabola- 4, EduRev gives you an ample number of Online tests for practice

Top Courses for JEE

Download as PDF

Top Courses for JEE

Important Questions for Parabola- 4

Find all the important questions for Parabola- 4 at EduRev.Get fully prepared for Parabola- 4 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Parabola- 4 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Parabola- 4 resources.

Parabola- 4 MCQs with Answers

Prepare for the Parabola- 4 within the JEE exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Parabola- 4

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Parabola- 4 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup