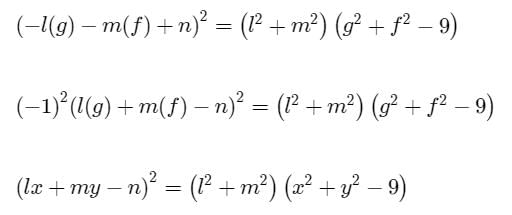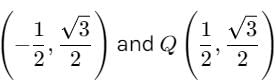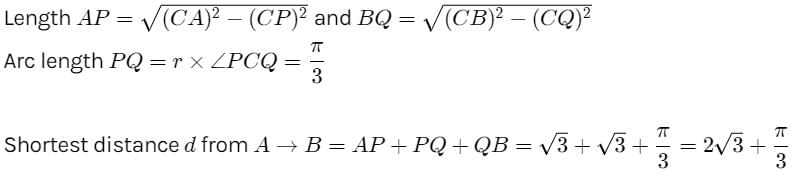Test: Circles - 5 - JEE MCQ
25 Questions MCQ Test - Test: Circles - 5
The equation of the circle which touches the axis of y at the origin and passes through (3, 4) is
The equation to the circle whose radius is 4 and which touches the negative x-axis at a distance 3 units from the origin is
Number of different circles that can be drawn touching 3 lines, no two of which are parallel and they are neither coincident nor concurrent, are
If a circle of constant radius 3k passes through the origin `O' and meets co-ordinate axes at A and B then the locus of the centroid of the triangle OAB is
A pair of tangents are drawn from the origin to the circle x2 + y2 + 20(x + y) + 20 = 0. The equation of the pair of tangents is
The locus of the centre of a circle which touches externally the circle, x2 + y2 – 6x – 6y + 14 = 0 and also touches the y-axis is given by the equation
The common chord of two intersecting circles C1 and C2 can be seen from their centres at the angles of 90º and 60º respectively. If the distance between their centres is equal to √3 + 1 then the radius of C1 and C2 are
A circle touches a straight line lx + my + n = 0 and cuts the circle x2 + y2 = 9 orthogonally, The locus of centres of such circles is
The length of the common chord of circles x2 + y2 – 6x – 16 = 0 and x2 + y2 – 8y – 9 = 0 is
If the two circles, x2 + y2 + 2g1x + 2f1y = 0 and x2 + y2 + 2g2x + 2f2y = 0 touches each other, then
If ,
,
&
are four distinct points on a circle of radius 4 units then, abcd =
What is the length of shortest path by which one can go from (–2, 0) to (2, 0) without entering the interior of circle, x2 + y2 = 1
Three equal circles each of radius r touch one another. The radius of the circle touching all the three given circle internally is
In a right triangle ABC, right angled at A, on the leg AC as diameter, a semicircle is described. The chord joining A with the point of intersection D of the hypotenuse and the semicircle, then the length AC equals to
The circle passing through the distinct points (1, t), (t, 1) & (t, t) for all values of `t'. passes through the point
The locus of the mid points of the chords of the circle x2 + y2 – ax – by = 0 which subtend a right angle at is
A circle is inscribed into a rhombus ABCD with one angle 60º. The distance from the centre of the circle to the nearest vertex is equal to 1. If P is any point of the circle, then | PA |2 + | PB |2 + | PC |2 + | PD |2 is equal to
Number of points (x, y) having integral coordinates satisfying the condition x2 + y2 < 25 is
Circles are drawn touching the co-ordinate axis and having radius 2, then
For the circles S1 º x2 + y2 – 4x – 6y – 12 = 0 and S2 º x2 + y2 + 6x + 4y – 12 = 0 and the line L º x + y = 0
3 circle of radii 1, 2 and 3 and centres at A, B and C respectively, touch each other. Another circle whose centre is P touches all these 3 circles externally. and has radius r. Also ∠PAB = q & ∠PAC = a.
Slope of tangent to the circle (x – r)2 + y2 = r2 at the point (x, y) lying on the circle is
The centre(s) of the circle(s) passing through the points (0, 0), (1, 0) and touching the circle x2 + y2 = 9 is/are
Point M moved along the circle (x – 4)2 + (y – 8)2 = 20. Then it broke away from it and moving along a tangent to the circle cuts the x-axis at the point (–2, 0). The co-ordinates of the point on the circle at which the moving point broke away can be