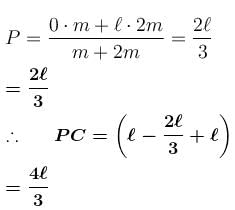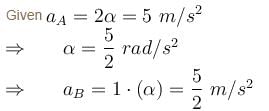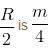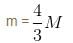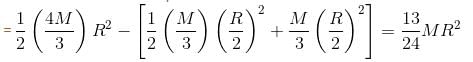Rigid Body Dynamics NAT Level - 1 - Physics MCQ
10 Questions MCQ Test - Rigid Body Dynamics NAT Level - 1
A solid sphere rolls down an inclined plane without slipping. The fraction of its total energy associated with its translation motion is :
If the radius of the earth becomes half of its present value, with its mass remaining the same, the duration of one day will become (in hours).
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is a rest in a horizontal position the value of tension in two strings 



A solid sphere and a solid cylinder having the same mass and radius, roll down the same incline. The sum of their acceleration (in ms–2) will be :
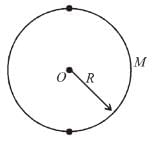
A disc of mass M and radius R = 3m is suspended in a vertical plane by a horizontal axis passing through its centre. After sticking an object of same mass M at its rim the mass is raised to the position of maximum height. Now this unstable system is released. When the object passes the position right below the centre of angular velocity (in ms–2) of the system would be :
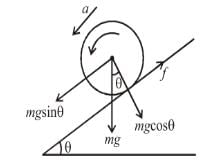
A uniform disc m and radius R is rolling down a rough inclined plane which makes an angle 30° with the horizontal. If the coefficient of static and kinetic friction are each to µ and the only forces acting are gravitational and frictional, then the magnitude of the frictional force acting on the disc is given by mg/a. Find the value of α?
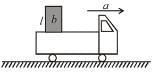
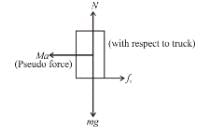
A box of dimensions ℓ = 4m and b = 2m is kept on a truck moving with an acceleration a. If box does not slide. Maximum acceleration in ms–2 for it to remain in equilibrium (w.r.t truck) is : (Take g = 10 ms–2)
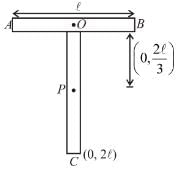
A T shaped object with dimensions shown in the figure, is lying on a smooth floor. A force 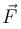 is applied at the point P parallel to AB, such that the object has only the translation motion without rotation. Find the location of P with respect to C in meter, when ℓ = 3m:
is applied at the point P parallel to AB, such that the object has only the translation motion without rotation. Find the location of P with respect to C in meter, when ℓ = 3m:
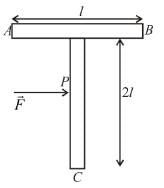
In the pulley system shown, if radii of the bigger and smaller pulley are 2m and 1m respectively and the acceleration of block A is 5 m/s2 in the downward direction, then the acceleration (in ms–2) of block B will be :
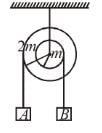
A hole of radius R/2 is cut from a thin circular plate of radius R as shown in the figure. If the mass of the remaining plate is M then find moment of inertia in kgm2 of the plate about an axis through O perpendicular to plane, when R = 6m, M = 2kg?


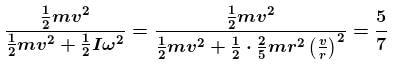
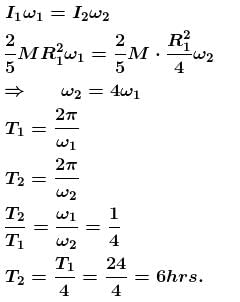
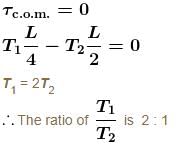
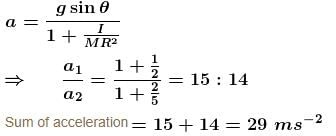
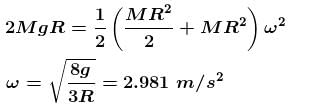

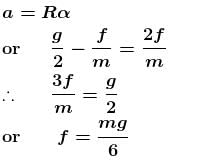
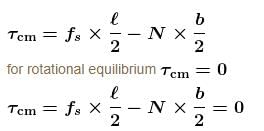
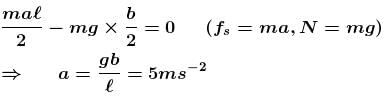
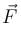 is applied at centre of mass of system.
is applied at centre of mass of system.