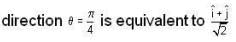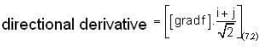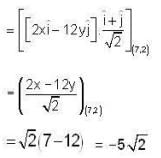IIT JAM Mathematics Practice Test- 9 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 9
Force 3i + 2j + 5k and 2i + j - 3k are acting on a particle and displace it from the point 2i - 2j + 10k, then the work done by the force is
Let 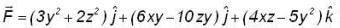 be a vector point function and C be the an Arc from (1,0, 1) to (3, 4, 5) of the curve, which is the intersection of the surface Z2 = x2 + y2 and Z = y + 1, then the value of
be a vector point function and C be the an Arc from (1,0, 1) to (3, 4, 5) of the curve, which is the intersection of the surface Z2 = x2 + y2 and Z = y + 1, then the value of 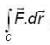 is
is
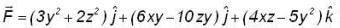 be a vector point function and C be the an Arc from (1,0, 1) to (3, 4, 5) of the curve, which is the intersection of the surface Z2 = x2 + y2 and Z = y + 1, then the value of
be a vector point function and C be the an Arc from (1,0, 1) to (3, 4, 5) of the curve, which is the intersection of the surface Z2 = x2 + y2 and Z = y + 1, then the value of 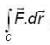 is
isForce of magnitude 5 units acting along the vector 2i - 2j + k displaces the point of application from (1, 2, 3) to (5, 3, 7), then the work done is
The value of line integral 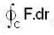 , where F = (x- 3y, 2x- y, 0) and C is the ellipse x2/9 + y2/4 = 1 in the XY plane described in the positive sense.
, where F = (x- 3y, 2x- y, 0) and C is the ellipse x2/9 + y2/4 = 1 in the XY plane described in the positive sense.
The value of line integral 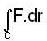 where F = xzi + yj +x2 k and C is the curve x = sinθ cosθ, y = sin2 θ, z = cos θ with θ increasing from 0 to π/2, is
where F = xzi + yj +x2 k and C is the curve x = sinθ cosθ, y = sin2 θ, z = cos θ with θ increasing from 0 to π/2, is
If u = 3x2y and v = xz2 - 2y. then grad [(gradu). (gradv)] is
The values of a, b, c so that the function
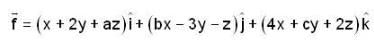 is irrotational.
is irrotational.
The value of 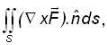 where
where 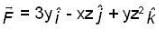 and S is the surface of the paraboloid Z = x2 + y2 bounded by Z = 4 and C is the boundary cuive described in the positive sense.
and S is the surface of the paraboloid Z = x2 + y2 bounded by Z = 4 and C is the boundary cuive described in the positive sense.
If F = xy2 i + 2x2 yz j - 3yz2 k , then curl F at (1 ,-1,1) is
If f = (x + y + 1) i + j + (-x -y) k , then f. curl f =
Let  and S is the surface of a rectangle bounded 0
and S is the surface of a rectangle bounded 0 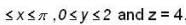 Then the value of
Then the value of 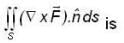
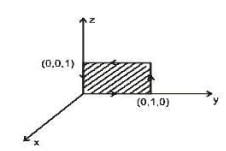
Let 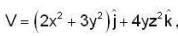 for a square surface shown in the figure, then
for a square surface shown in the figure, then 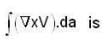
If 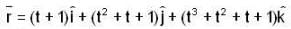 then which one of the following is /are true?
then which one of the following is /are true?
if 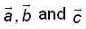 are three non - zero vector’s, then which of the following(s) is/are false statements ?
are three non - zero vector’s, then which of the following(s) is/are false statements ?
if 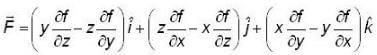 and
and 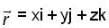 with r =
with r = 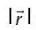 then which of the followings is /are true ? (where f be a SPF).
then which of the followings is /are true ? (where f be a SPF).
If the scalar function is f = x2yz3 then at that point (2,1,-1)
A particle acted on by constant forces 4i + j - 3k and 3i + j - k is displaced from the point i + 2j + 3k to the point 5i + 4j + k. The total work done by the force is _____.
The value of line integral  where F = x2y2 i + yj and cuive C is y2 = 4x in the xy-plane from (0, 0) to (4, 4), where r = xi + yj, is _____
where F = x2y2 i + yj and cuive C is y2 = 4x in the xy-plane from (0, 0) to (4, 4), where r = xi + yj, is _____
The value of 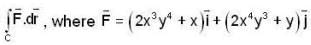 and C is given by
and C is given by  is __________.
is __________.
The directional derivative of f = xyz2 at (1,0, 3) in the direction of the vector i - j + k is _________.
The angle between the surface x2 + y2 + z2 = 9 and x2 + y2 - z = 3 at the point (2, -1, 2), i s ________.
The directional derivatives of f = x2 + y2 + z2 at (1,2, 3) in the direction of the line x/3 = y/4 = z/5, i s ________.
If vector A = ( ax + 3y + 4 z ) i + ( x - 2y + 3z) j + ( 3x + 2 y - z) k is solenoidal, then a is ______ .
If the vector 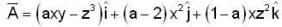 has its curl identically equal to zero,then the value of a is _________ .
has its curl identically equal to zero,then the value of a is _________ .
A particle moves anticlock wise along the curve x2 + y2 = 9 from (3,0) to a point Q under the force action 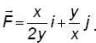 Then the total no. of possible locations of Q so that the work done is equal to 3/2 is ______.
Then the total no. of possible locations of Q so that the work done is equal to 3/2 is ______.
The directional derivative of f(x, y) = x2 - 6y2 at the point (7, 2) in the direction 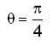 is _____________.
is _____________.


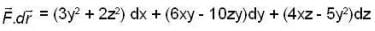
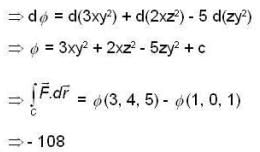

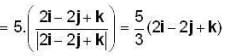
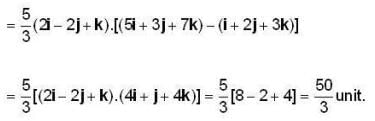
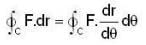
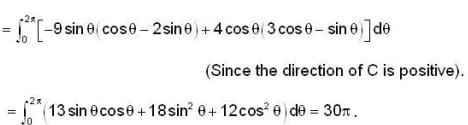
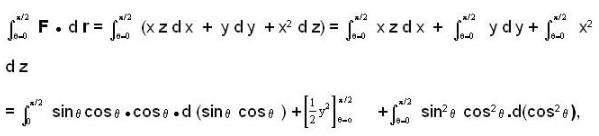
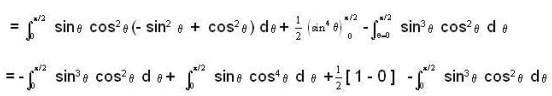 =
= 
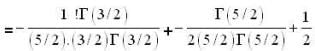
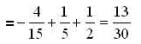
 then the value of
then the value of 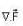 is
is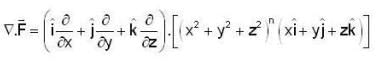
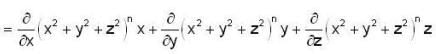
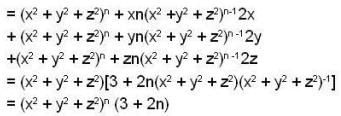
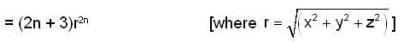

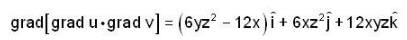
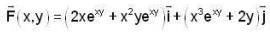
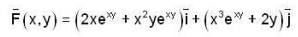 Here is P and Q as well as the appropriate derivatives.
Here is P and Q as well as the appropriate derivatives.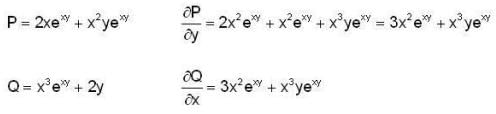
 be a vector field on an open and simply-connected region D
be a vector field on an open and simply-connected region D
 f is conservative.
f is conservative.
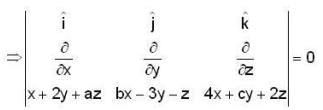
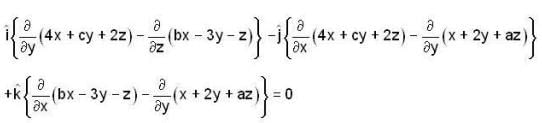
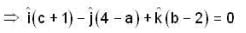
 are independent vectors, so their coefficients must be zero separately, i.e.,
are independent vectors, so their coefficients must be zero separately, i.e.,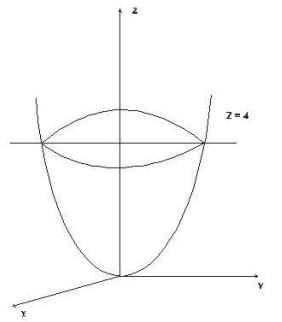
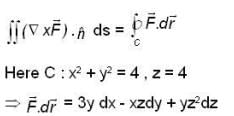
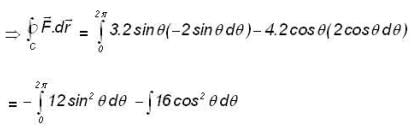
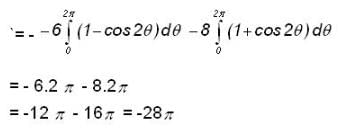
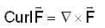
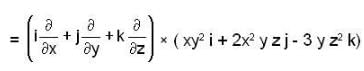
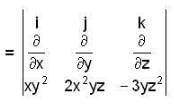
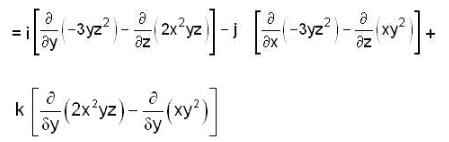
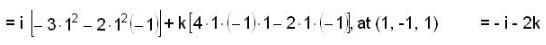
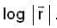
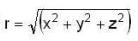
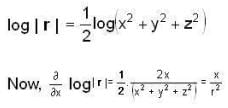
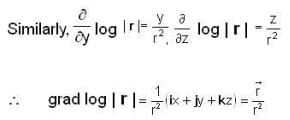
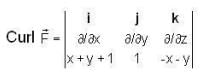
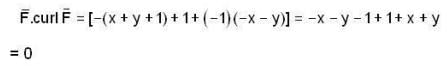
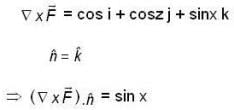
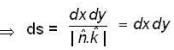
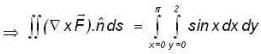
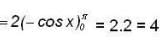
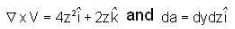
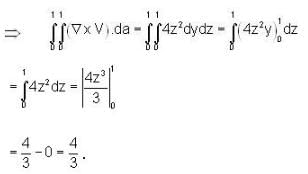
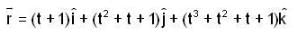
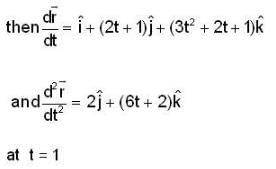
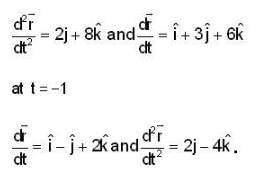
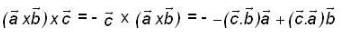

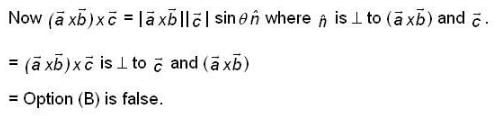
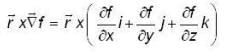
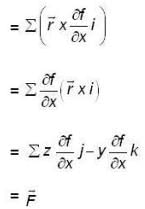

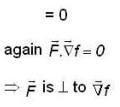
 then
then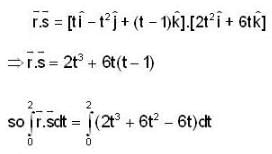
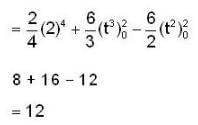
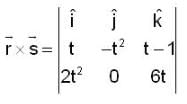
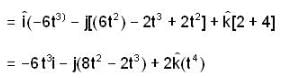 Hence
Hence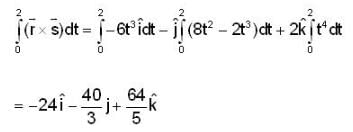
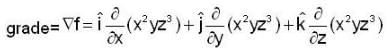

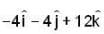

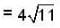
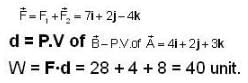
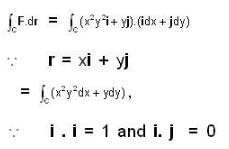
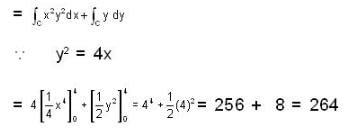
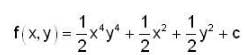
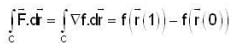
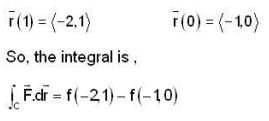
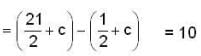
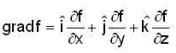
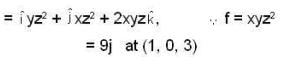
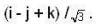
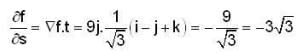
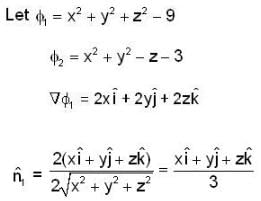
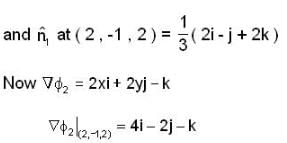
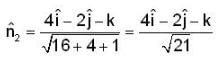
 at ( 2 , -1 , 2 ) be
at ( 2 , -1 , 2 ) be 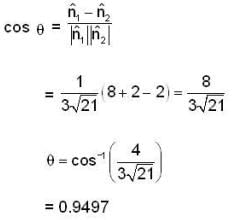
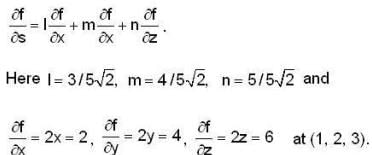
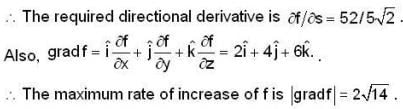
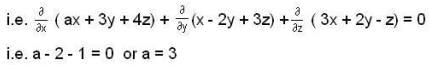
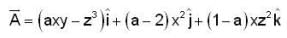
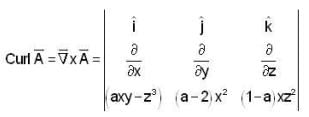
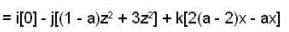
 is identically equal to zero , then all three components of
is identically equal to zero , then all three components of 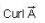 are zero
are zero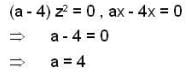
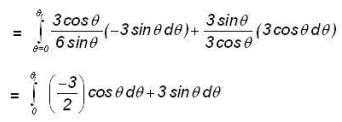
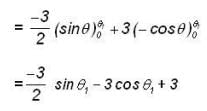
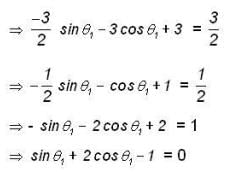
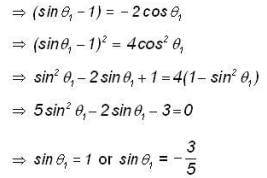 Here both the values are possible .
Here both the values are possible .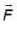 is equal to 3/2
is equal to 3/2