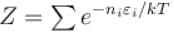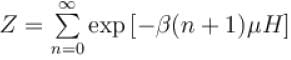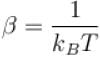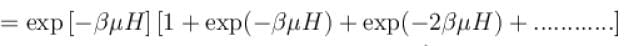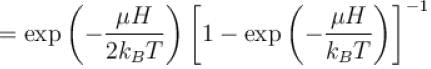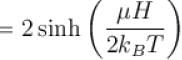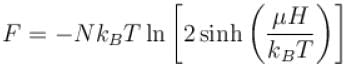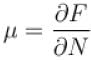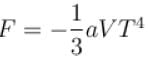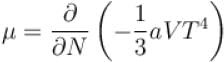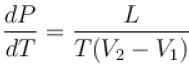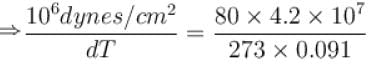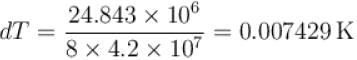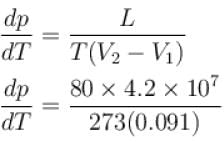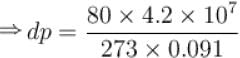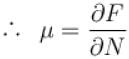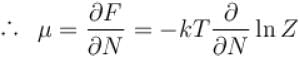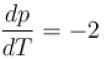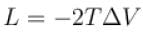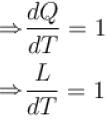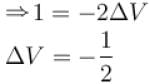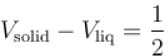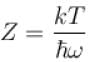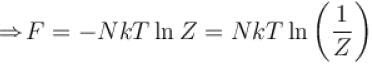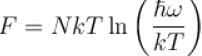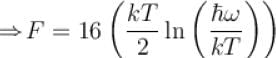Thermodynamic Potential NAT Level – 1 - IIT JAM MCQ
10 Questions MCQ Test - Thermodynamic Potential NAT Level – 1
A system of N localized, non-interacting spin 1/2 ions of magnetic moment in each is kept in an external magnetic field H. If the system is in equilibrium at temperature T, the Helmholtz free energy of the system is given as  Calculate the value of α?
Calculate the value of α?
 Calculate the value of α?
Calculate the value of α?The free energy of a photon gas enclosed in a volume V is given by 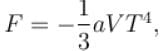 where a is the constant and T is the temperature of the gas.
where a is the constant and T is the temperature of the gas.
The chemical potential of the photon gas is?
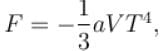 where a is the constant and T is the temperature of the gas.
where a is the constant and T is the temperature of the gas.The chemical potential of the photon gas is?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Calculate the standard Gibb’s free energy change for the formation of methane from carbon and hydrogen at 298 K in the units of kJ/mol. Given that ΔH is –74.9 kJ/mol and ΔS = -80.75J{\rm{/K - mol}}.\)
Calculate the depression of melting point of ice (in K) produced by 1 atm increase of pressure, given that Lice = 80 cal gm-1 and specific volume of ice and water at 0°C are 1.091 cm3 and 1 cm3 respectively
To change the melting point of ice by 1K, what should be the change in the pressure, given that L = 80 cal gm-1 and specific volume of ice and water at 0°C are 1 cm3 and 1.091 cm3 respectively. Give your answer in atm.
Calculate the value of ΔH for an isothermal process?
If Z be the partition function and N represent number of particles the chemical potential is given as 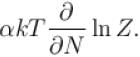 Find the value of α.
Find the value of α.
A solid melts into liquid. The relation between the pressure p and the temperature T of the phase transition is P = –2T + P0 , the entropy charge associated with the phase transition is 1 Joule mol-1 K-1 . The Claussius-Clapeyron equation for the latent heat latent heat 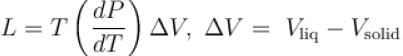 then
then 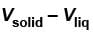 is equal to?
is equal to?
It the partition function of a harmonic oscillator with frequency at temperature T in 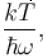 then the free energy of 8 such independent oscillators in terms of
then the free energy of 8 such independent oscillators in terms of 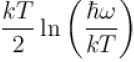 is
is
A system of N non-interacting and distinguishable particles of spin1 is in thermodynamic equilibrium. The entropy of the system turns out to be of the form NkBln x. Find the value of x?