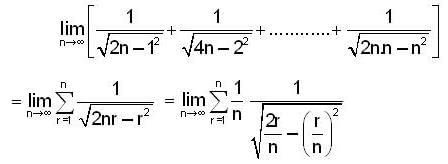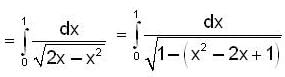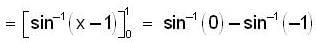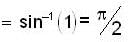IIT JAM Mathematics Practice Test- 14 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 14
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The value of integral 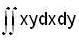 over the region in the positive quadrant for which x + y ≤ 1, is
over the region in the positive quadrant for which x + y ≤ 1, is
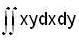 over the region in the positive quadrant for which x + y ≤ 1, is
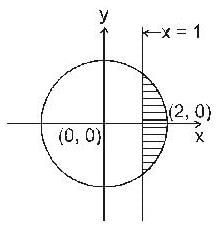
over the region in the positive quadrant for which x + y ≤ 1, isThe area of smaller part between the circle x2 + y2 = 4 and line x = 1 is
The area bounded by curve, y = x2 and y = 2 - x2 is
The volume of the region bounded by the surfaces y = x2, x = y2 and the planes z = 0, z = 3 is,
The area of largest part between the circle x2 + y2 = 8 and the line is x+y = 2√2 is,
Area bounded by the curve xy - 3x - 2y -10 = 0, x-axis and the lines x = 3,x = 4 is
The value of the double integral 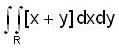 where R = [0 ,1 ; 0, 3] and [ x + y ] denotes the greatest integer less than or equal to (x + y) is,
where R = [0 ,1 ; 0, 3] and [ x + y ] denotes the greatest integer less than or equal to (x + y) is,
The area of the loop of the curve ay2 = x2(a - x) is
The length of the arc of the curve
x sinθ + y cosθ = f'(θ)
x cosθ - y sinθ = f"(θ) is given by
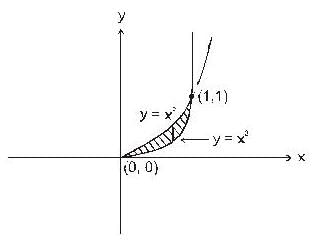
Evaluate 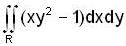 were R is bounded by y = x2 and y = x3
were R is bounded by y = x2 and y = x3
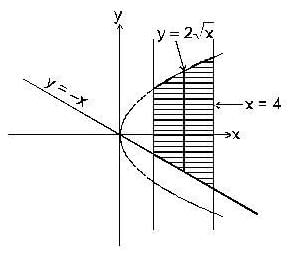
The area bounded by the curves 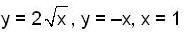 and x = 4 is given by
and x = 4 is given by
Which of the following is the volume generated by rotating the area bounded by 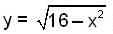 and y = 2 about the x - axis ?
and y = 2 about the x - axis ?
Let F : R → R be a continuous function and a > 0. Then tine integral 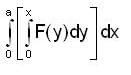 is equal to
is equal to
Find the length of the arc of the semi cubical parabola ay2 = x3 from its vertex to the point (a, a).
Let 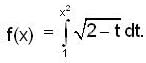 then the total no. of real distinct roots of the equation x2 - f'(x)= 0 is
then the total no. of real distinct roots of the equation x2 - f'(x)= 0 is
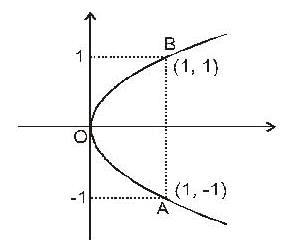
Compute the integral 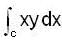 along the arc of the parabola x = y2 fro m (1 , - 1 )to(1, 1)
along the arc of the parabola x = y2 fro m (1 , - 1 )to(1, 1)
By changing the order of integration, the integral  can be represented as
can be represented as  determine the value of A.
determine the value of A.


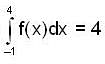 and
and  then the value of
then the value of 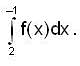


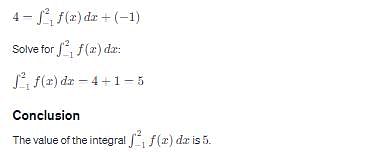
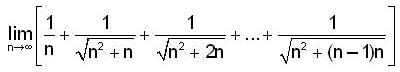 is equal to
is equal to 
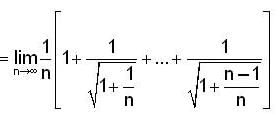
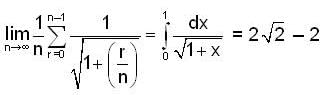
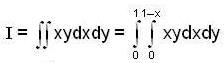
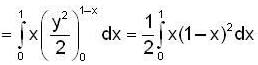
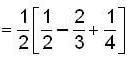
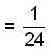
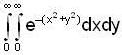
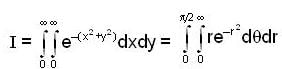
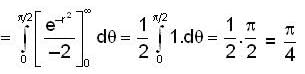


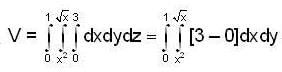
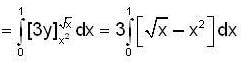
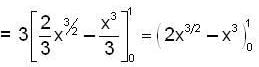
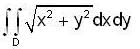 where
where  is;
is;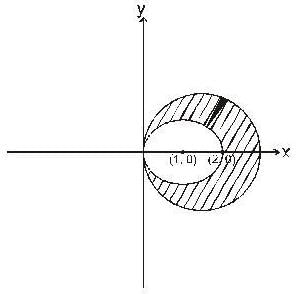
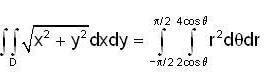
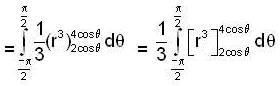
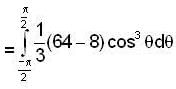
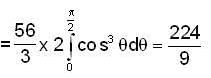
 then f'(4) is equal to
then f'(4) is equal to 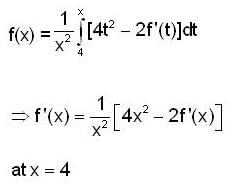
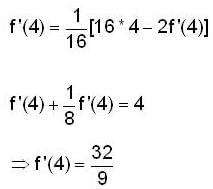
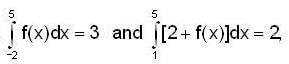 then the value of
then the value of 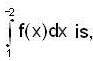
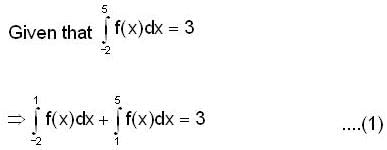
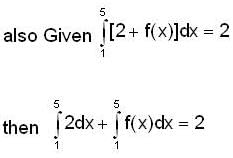

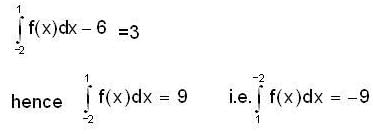
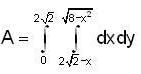
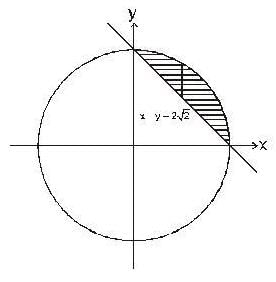
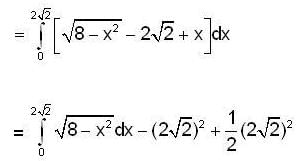
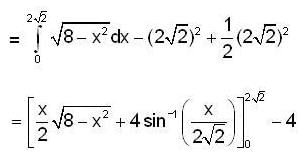
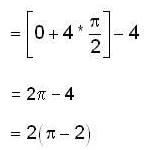
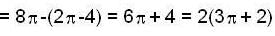
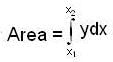
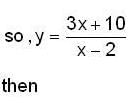
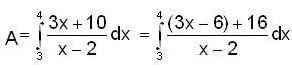
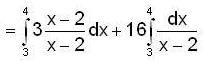
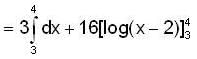
 is
is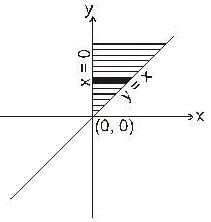
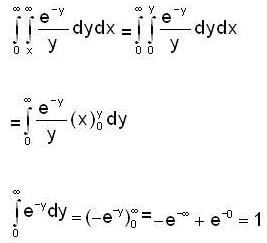
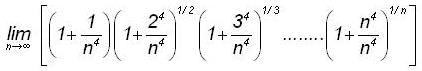
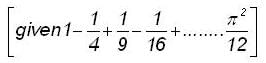
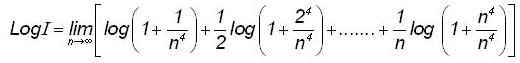
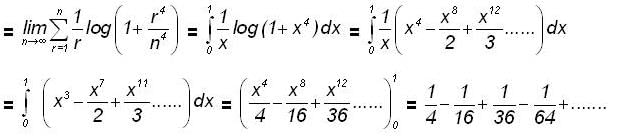
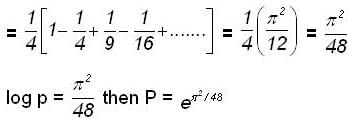
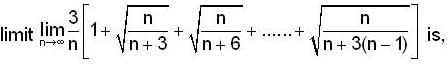
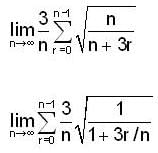
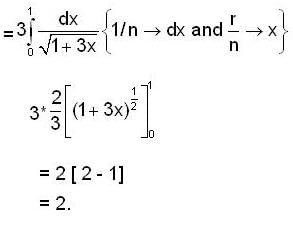

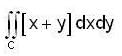
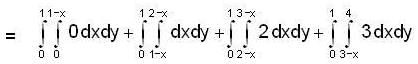

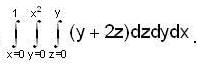
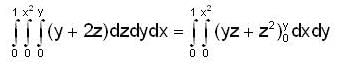
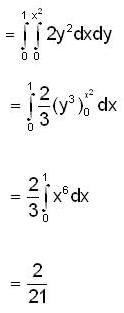
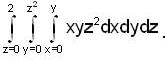
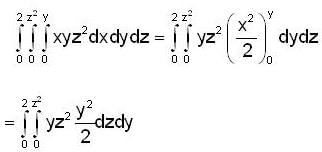
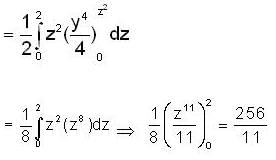
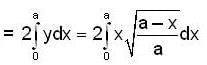
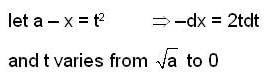
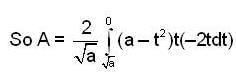
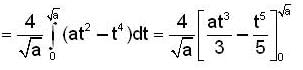
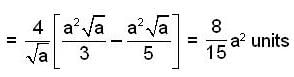
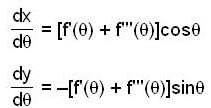
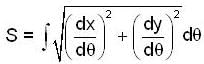
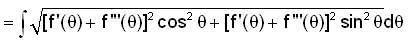
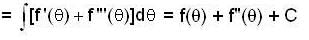
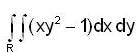
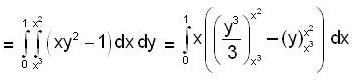
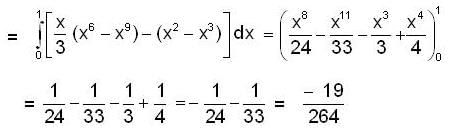
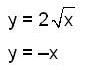

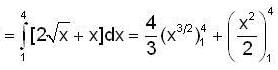
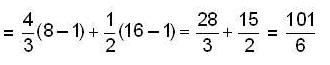

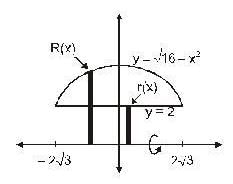
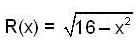 and r(x) = 2
and r(x) = 2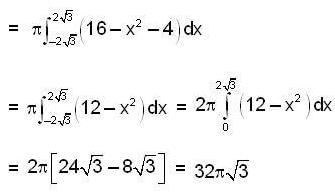
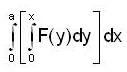 this integral is not solvable.
this integral is not solvable.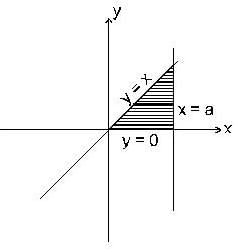
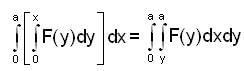
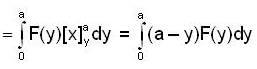
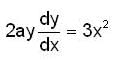
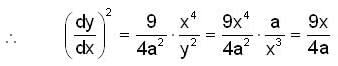
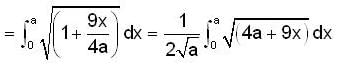


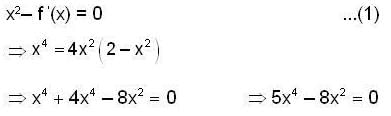
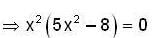
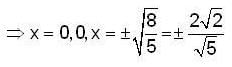
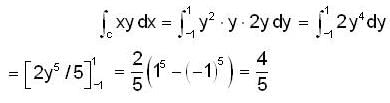
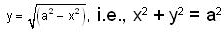 and the straight line y = x +2a. The limits of x are given by the straight lines x = 0 and x = a
and the straight line y = x +2a. The limits of x are given by the straight lines x = 0 and x = a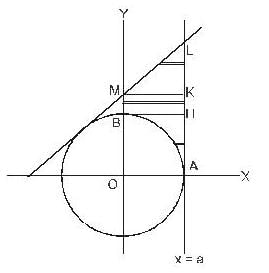

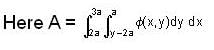
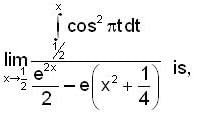
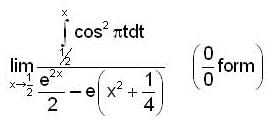
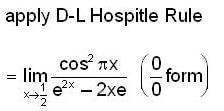
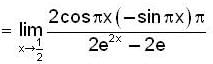
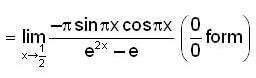
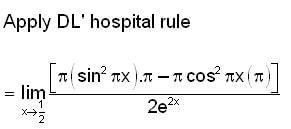
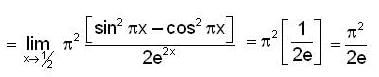
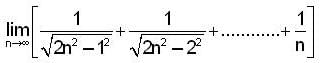 is equal to
is equal to