Linear Algebra NAT Level - 1 - IIT JAM MCQ
10 Questions MCQ Test - Linear Algebra NAT Level - 1
What is the maximum value of λ, for which the given system is inconsistent?
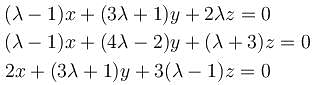
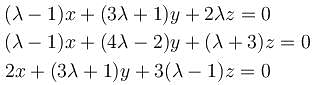
Given a matrix, 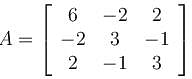
What would be the sum of eigenvalues of A–1? (Give the answer upto 3 decimal places )
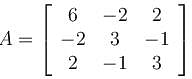
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
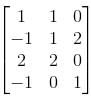
Consider the matrix  Then find the product of eigenvalues?
Then find the product of eigenvalues?
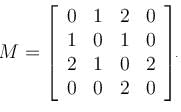 Then find the product of eigenvalues?
Then find the product of eigenvalues?The three equations,
–2x + y + z = a
x – 2y + z = b
x + y – 2z = c
has
Consider the following equations
x + y – 3z + 2w = 0
2x – y + 2z – 3w = 0
3x – 2y + z – 4w = 0
–4x – y + 3z + 4w = 0
Find the rank of the coefficient matrix.
If x = y = z = αc satisfy the matrix equation AX = 0 where
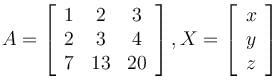
then find the value of α.
For which value of λ will the following equations fail to have unique solution?
3x – y + λz = 1
2x + y + z = 2
x + 2y – λz = –1
Let A be a 3 × 3 matrix with eigen values 1, –1, 0. Then the determinant of I + A100 is :
The system of equations αx + y + z = α - 1, x + αy + z = α - 1, x + y + αz = α - 1 has no solution. Find the maximum value of α


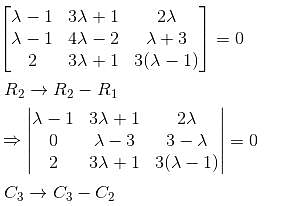
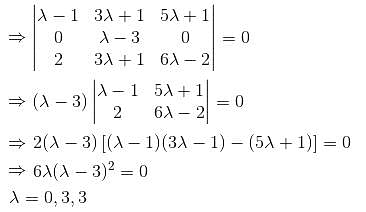
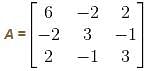

 are the eigenvalues of A, then
are the eigenvalues of A, then 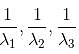 will be the eigenvalues of A–1.
will be the eigenvalues of A–1.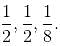

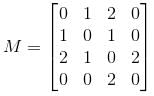
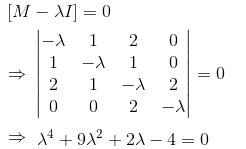

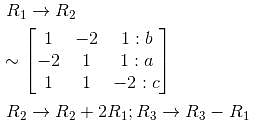

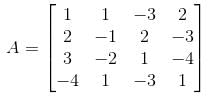
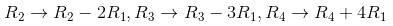
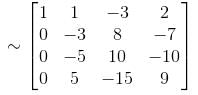
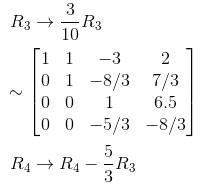
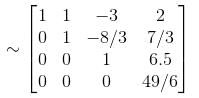
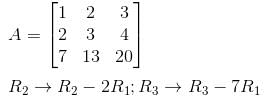

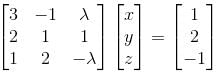
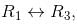 we get
we get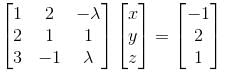
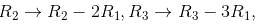 we get
we get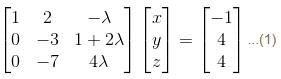
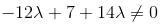
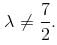
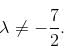 In case of
In case of 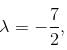 the equation (1) becomes
the equation (1) becomes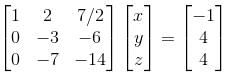
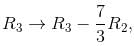 we get
we get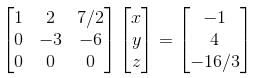
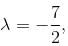 no solution exists.
no solution exists.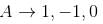
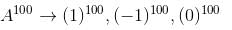
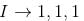
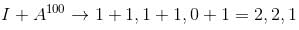
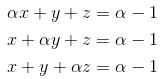
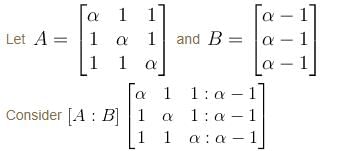
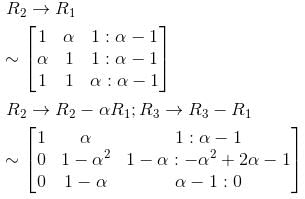
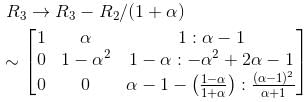
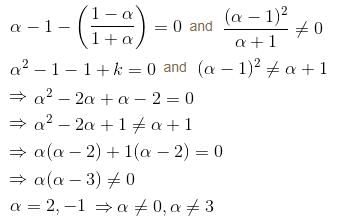
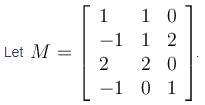 Then the rank of M is equal to :
Then the rank of M is equal to :