Complex Number MCQ Level - 2 - IIT JAM MCQ
10 Questions MCQ Test - Complex Number MCQ Level - 2
The point of intersection the curves
arg ( z - i + 2 ) = 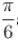 and arg ( z + 4 - 3i ) =
and arg ( z + 4 - 3i ) = 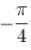 is given by
is given by
arg ( z - i + 2 ) =
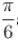 and arg ( z + 4 - 3i ) =
and arg ( z + 4 - 3i ) = 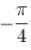 is given by
is given byIf 1, α1,α2,α3.........and α8 re nine, ninth roots of unity (taken in counter-
clockwise sequence) then | ( 2 - α1 ) (2 - α3) ( 2 - α5 ) ( 2 - α7 ) | is equal to :
clockwise sequence) then | ( 2 - α1 ) (2 - α3) ( 2 - α5 ) ( 2 - α7 ) | is equal to :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If 'z' is complex number then the locus of ‘z’ satisfying the condition
|2z - 1| = | z - 1 | is
|2z - 1| = | z - 1 | is
If t and c are two complex numbers such that | t | = 1 and z = 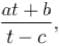 z = x + iy , Locus of z is (where a, b are complex numbers)
z = x + iy , Locus of z is (where a, b are complex numbers)
If ω is an imaginary cube root of unity, then (1+ ω - ω2 )7 is equal to
If a complex number z satisfies | 2z + 10 + 10i | < 5 √3 - 5, then the least principal argument of z is.
Image of the point, whose affix is 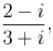 in the line (1 + i ) z + ( 1 - i )
in the line (1 + i ) z + ( 1 - i ) 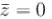 is the point whose affix is :
is the point whose affix is :
Let S denote the set of all complex numbers z satisfying the inequality |z - 5i| < 3.The complex numbers z in S having least positive argument is :
Number of solution of the equation 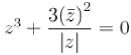 where z is a complex number is :
where z is a complex number is :


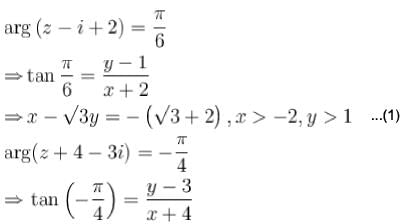
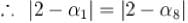
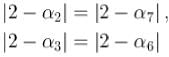
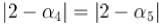
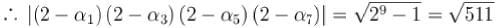

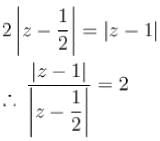
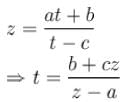
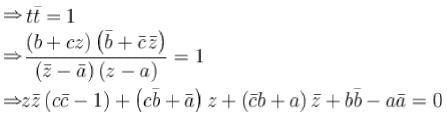
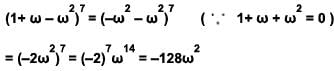









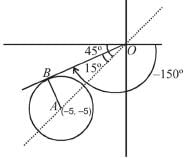


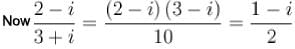
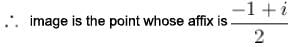
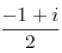
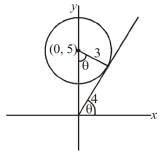
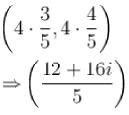
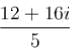

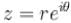
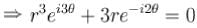
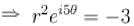
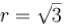 and 5 distinct value o f 'O'
and 5 distinct value o f 'O'














