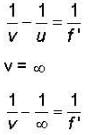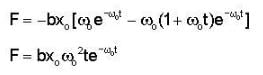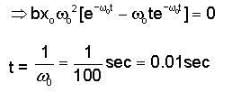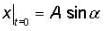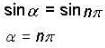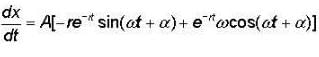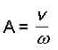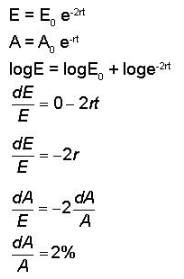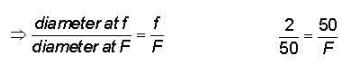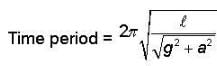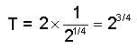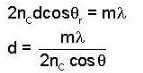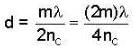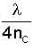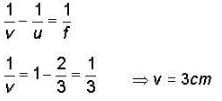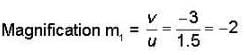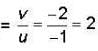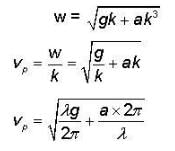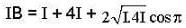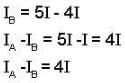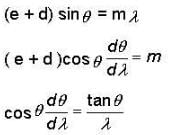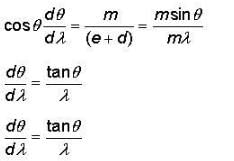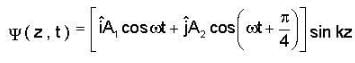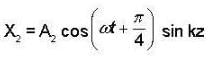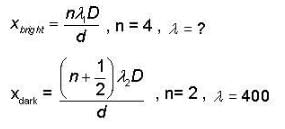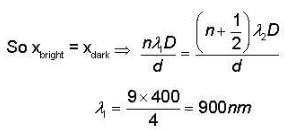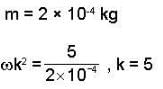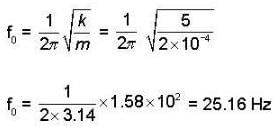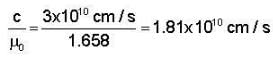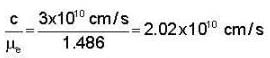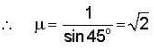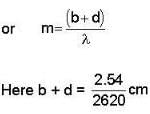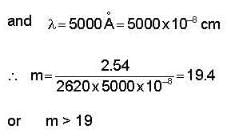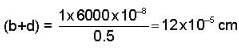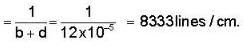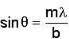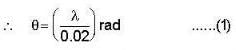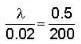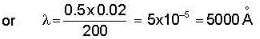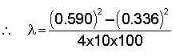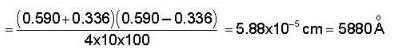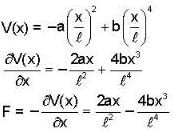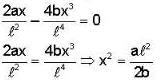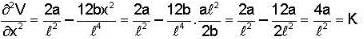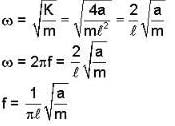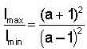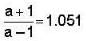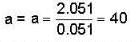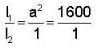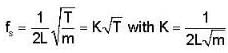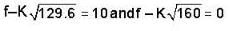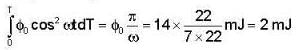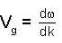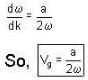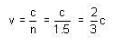JAM-20-PH-VTP-2 (SET-1)-FINAL - IIT JAM MCQ
30 Questions MCQ Test - JAM-20-PH-VTP-2 (SET-1)-FINAL
A simple pendulum is set - up in a trolley which moves to the right with an acceleration 'a' on a horizontal plane, then the thread of the pendulum in the mean position makes an angle θ with the vertical
A combination of two thin convex lenses of equal focal lengths is kept separated along the optic axes by a distance of 20 cm between them. The combination behaves as a lens system of infinite focal length. If an object is kept at 10 cm from the first lens. Its image will be formed on the other side at a distance x from the second lens. The value of x is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A spring mass system has undamped natural angular frequency ω0 = 100 rad S-1. The solution x(t) at critical dam ping is given by x(t) = x0 (1 + ω0t) exp(-ω0t) where x0 is a constant. The system experiences the maximum damping force at time .
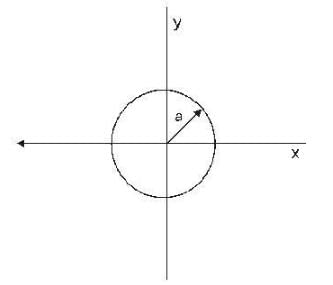
W hen two sim ple harmonic oscillations rep resented by x = A0 cos(ωt + α) and y = B0 cos (ωt + β) are superposed at right angles, the resultant is a circle of radius as shown in the figure. The condition which corresponds to this are
The instantaneous position x(t) of a small block performing one dimensional damped oscillation is x(t) = Ae-rt sin (ωt + α). Here ω is the angular frequency,r is the damping coefficient. A is the initial amplitude and α is the initial phase . If Xt = 0 and  he values of A and α (with n = 0. 1, 2 , .........) are
he values of A and α (with n = 0. 1, 2 , .........) are
A lightly damped harmonic oscillator losses energy at the rate of 4% per minute. The decrease in amplitude of the oscillator per minute will be closest to
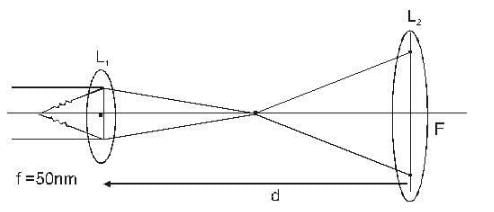
A collimated beam of light of diameter 2nm is propagating along the x - axis. The beam is to be expanded to a collimated beam of diameter 50nm using a combination of the convex lenses. A lens of focal length of 50nm and another lens with focal length f are to be kept at a distance a between them. The value of F and d respectively are
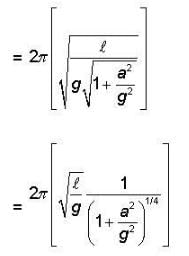
A simple pendulum suspended from the ceiling of a stationary. Cart has a time period 2 seconds when the cart accelerates in the horizontal direction with an accelerates in the horizontal direction with an acceleration of 10 m/s2, the time period of the pendulum is (g = 10 m /see2)
A glass plate P (refractive index np, = 1.54) is coated with a dielectric material C with the refractive index nc = 1.6. In order to have enhanced reflection from this coated glass for near normal incident light of wavelength λ, the thickness of the coating material. C must be
Two thin convex lenses ℓ1, and ℓ2 with focal lengths 1 cm and 2 cm respectively are separated by a distance of 4 cm along their axis as shown below.
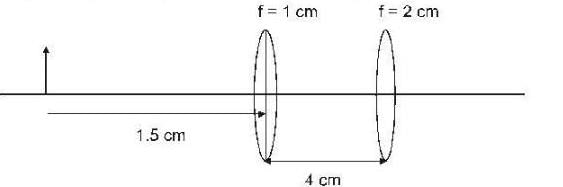
An object is placed at a distance of 1.5 cm before the first lens. The ratio of the final image size to the object size is
The dispersion relation for deep water is given by ω2 = gk + ak3, where g and a are constants.
The phase velocity in terms of λ is
Two beams of light having Intensities I and 4I interfere to produce a fringe pattern on a screen. The phase difference between the beams is π/2 at point A and π at point B ,then the difference between the resultant intensities A and B is
Consider a plane transmission diffraction grating, let d be the distance between ruled lines, m the order number and θ the observation angle. The angular dispersion for incident light of wavelength λ is
Which one of the following is a elliptically perpendicularly polarized standing wave ?
In a double slit experiment two parallel slits are illuminated first by light of wavelength 400 nm and then by light of unknown wavelength. The fourth order dark fringe resulting from the known wavelength of light falls in the same place on the screen as the second order bright fringe from the unknown wave length. The value of unknown wavelength of the light is
The equation of motion is  = 0.124 sin100t, where ail quantities are in S.l. units, then natural frequency of undamped oscillation is
= 0.124 sin100t, where ail quantities are in S.l. units, then natural frequency of undamped oscillation is
The velocity of extraordinary ray in calcite crystal in a plane perpendicular to the optic axis. Given μ0 =1.658, μe = 1.486 and c = 3x1010 cm/s.
The critical angle of light in a certain substance is 45°. What is the polarizing angle?
How many orders will be visible if the wavelength of incident radiation is 5000 Å and the number of lines on the grating is 2620 to an inch?
How many lines per centimetre are there in a plane transmission grating which gives 1st order of light of wavelength 6000 Å at angle of diffraction 30°?
In Fraunhofer diffraction due to a narrow slit, a screen is placed 2 m away from the lens to obtain the pattern. If the slit width is 0.2 mm and first minima lie 5 mm on either side of the central maximum, find the wavelength of light.
Newton’s rings are observed by keeping a spherical surface of 100 cm radius on a plane glass plate. If the diameter of the 15th bright ring is 0.590 cm and the diameter of the 5th ring is 0.336 cm, what is the wavelength of light used?
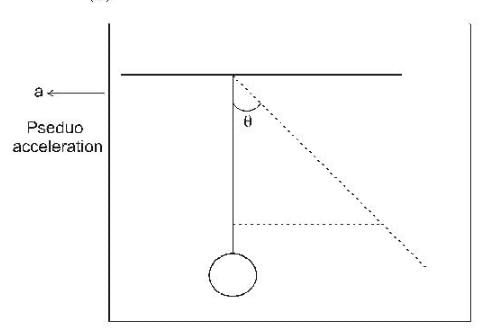
A particle of mass m moves in one dimension under the influence of a potential energy 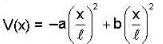 where a and b are positive constants and ℓ is a characteristic length. The frequency of small oscillation about a point of stable equilibrium is
where a and b are positive constants and ℓ is a characteristic length. The frequency of small oscillation about a point of stable equilibrium is
In an interference pattern with two coherent sources, the amplitude of intensity variation is found to be 5% of the average intensity. Calculate the relative intensities of the interfering sources.
A string under a tension of 129.6 N produces 10 beats per sec when is vibrated along with a tuning fork. When the tension in the string is increased to 160 N. it sounds in unison with the same tuning fork. Calculate the fundamental frequency of the tuning fork.
A beam of plane-polarized light falls on a polarizer which rotates about the axis of the ray with angular velocity ω = 22 rad/sec. Find the energy (mJ) of light passing through the polarizer per one revolution if the flux of energy of the incident ray is equal to φ = 14 mω.
The radius of curvature of curved surface of a plano-convex thin lens of refractive index n = 3 of focal length 0.4 m is
A pulse of electromagnetic radiation propagates through a normally dispersive medium. As it propagates, the pulse gets broadened. This is because
The dispersion relation for electromagnetic waves in a certain medium is given by ω2 = ak where a is a constant, ω the frequency and k the magnitude of the wave vector. The velocity of energy propagation in this medium is
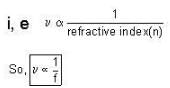
A fast charged particle passes perpendicularly through a thin glass sheet of refractive index 1.5. Inside the glass, the particle emits light. The minimum speed of the particle is



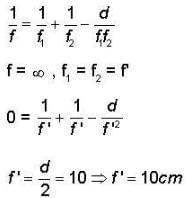

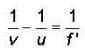
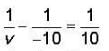 ⇒ v = ∞
⇒ v = ∞