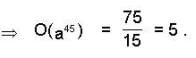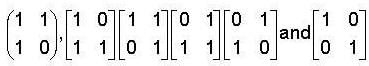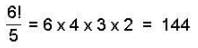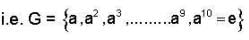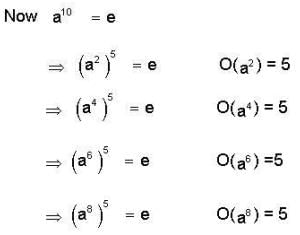IIT JAM Mathematics Practice Test- 16 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 16
Set s = { 1 , 2 , 3 , 4 , 5 } and let a permutation a = (1 2 3 ) (1 4 5 ) then a99 is equal to __________.
Find the smallest subgroup of z containing 8 and 14 both.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let G be a group of order 200, then the no. of subgroups of G of order 50 is
Given axa = b in a group G , where a,b ∈ G then x is equal to
If H be a subgroup of G, then H is normal in G, if
An element ap of a finite cyclic group G of order n is a generator of G if 0 < p < n and also
Let G = {e, a, a2, a3, b, ab, a2b, a3b} with a4 = e, b2 = e, ab = a-1b and H = {e, a2, ab, a3b}, K = {e, a3b}then which one of the following is false statement ?
The no. of elements of order 5 in a symmetric group S5 is
Let G be a group of order 77. then, the centre of G is isomorphic to
S5 be the permutation group on 5 symbols, then number of element in S5 such that a5 = a2
Which one of the following is smallest group ?
For any integer n > 2, how many elements in ∪(n) that satisfy X2 = 1
The no. o f cosets of H in G ,where G = ( Z , + ) and H = ( 8Z , + ) is
Which one of the following is a cyclic group ?
The order of abelian simple group should be
If H be normal in G such that 0 (H) and 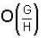 are co-prime then
are co-prime then
Let a be an element of a group G and 0(a) = 75 then find the order of the element a45.
Let G be a group with identity e such that for some a ∈ G , a2 ≠ e and a6 = e then which of the following is true ?
Let G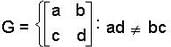 where a , b , c, d are integers modulo 2 } then
where a , b , c, d are integers modulo 2 } then
If H1 and H2 are two right cosets of subgroup H , then
Statement A: All cyclic groups are abelian.
Statement B: Every simple groups are cyclic.
If H and K are subgroups of order 6 and 8 respectively, then the minimum no. of elements of product set HK is
Find the total no. of non -isomorphic abelian group of order 32.
If order of any group G is 144 then find total no. of subgroup of group G.
Let G be a simple group of order 168. What is the no. of subgroups of G of order 7 ?
Find the total no. of elements of order 5 in a abelian group of order 10.


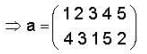
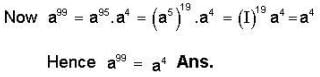
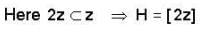

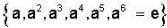 are
are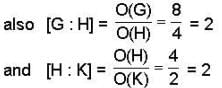

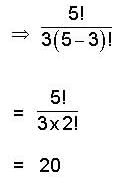
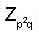 , where p is prime and p , q are distinct primes is p -1"
, where p is prime and p , q are distinct primes is p -1"
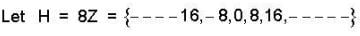


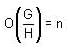
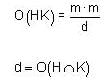
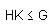
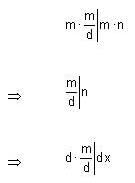
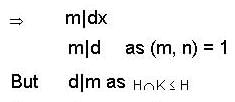


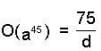 , where d =gcd (75, 45) = 15
, where d =gcd (75, 45) = 15