IIT JAM Mathematics Practice Test- 17 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 17
Let  are three arbitrary rector’s. Then the rector's
are three arbitrary rector’s. Then the rector's 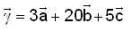 are
are
 are three arbitrary rector’s. Then the rector's
are three arbitrary rector’s. Then the rector's 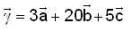 are
areThe unit vector normal to the surface x2y + 2xz = 4 at the point (2,-2,3) is
The derivative of f(x, y) at point (1, 2) in the direction of vector i + j is 2 √2 and in the direction of the vector - 2j is - 3 . Then derivative of f(x, y) in the direction - i - 2j is
The point at which the derivative of the function f(x,y) = x2 - xy - y + y2 vanishes along the direction 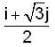 is
is
Let 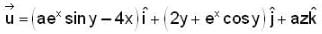 where a is a constant. If the line integral
where a is a constant. If the line integral 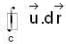 over every closed curve c is zero, then a is equal to
over every closed curve c is zero, then a is equal to
Let 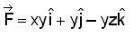 denote the force filed on a particle traversing the path L from (0,0,0) to (1,1,1) along the cuive of intersection of the cylinder y= x2 and the plane z = x the work done by
denote the force filed on a particle traversing the path L from (0,0,0) to (1,1,1) along the cuive of intersection of the cylinder y= x2 and the plane z = x the work done by 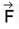 is
is
For a solenoidal vector field  which of the following is not true ?
which of the following is not true ?
If S be the surface of sphere x2 + y2 + z2 = 9.
the integral 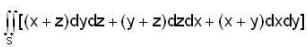 is equal to
is equal to
The value of surface integral 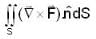 over the surface of the paraboloid z = 1 - x2 - y2, z > 0, where
over the surface of the paraboloid z = 1 - x2 - y2, z > 0, where 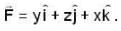
If the vector's 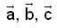 satisfy the condition
satisfy the condition 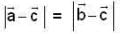 then
then 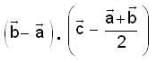 is equal to
is equal to
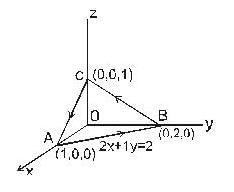
The line integral of the vector field, 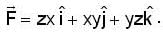 along the boundary of the triangle with vertices (1,0,0), (0,2,0), and (0,0,1), oriented anticlock wise, when viewed from the point (2,4,2) is
along the boundary of the triangle with vertices (1,0,0), (0,2,0), and (0,0,1), oriented anticlock wise, when viewed from the point (2,4,2) is
The value of integral
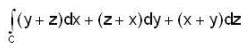
where C is the curve of intersection of the surface x2 + y2 + z2 = a2 bounded by the plane x + y + z = 0, is
The vector 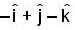 bisects the angle between the vectors
bisects the angle between the vectors 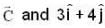 then the unit vector along
then the unit vector along 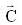
Let T be the smallest positive real no. such that the tangent to the helix
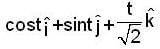
at t = T is orthogonal to the tangent at t = π/2
Then the line integral of 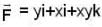 along the section of the helix from t = 0 to t = T is
along the section of the helix from t = 0 to t = T is
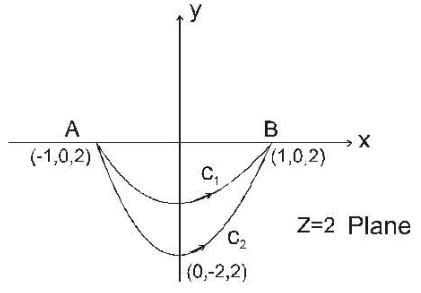
Let c1 : x2 + y2 = 1 and 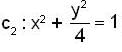 be the curves from (-1,0,2) to (1,0,2) drawn counter clock wise in the lower half (y ≤ 0) of the plane z = 2 and let
be the curves from (-1,0,2) to (1,0,2) drawn counter clock wise in the lower half (y ≤ 0) of the plane z = 2 and let 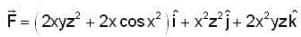 be a vector point function. Let the line integrals be
be a vector point function. Let the line integrals be 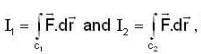 then
then
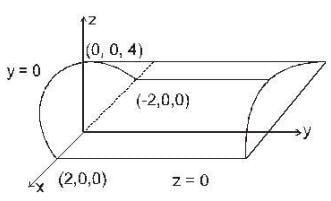
Let S be the boundary of the region consisting of the parabolic cylinder z = 4 - x2 and the planes y = 0 , y = 2 and z = 0 and  be a vector point function, then the value of
be a vector point function, then the value of 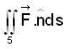 is
is
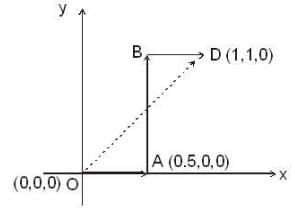
The work clone by the force 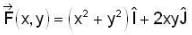 in moving a particle from the origin O ( 0 ,0 ,0 ) to the poin t D (1,1,0) on t h e z = 0 plane along the paths OABD as shown in the figure (where the coordinates are measured in meters) is,
in moving a particle from the origin O ( 0 ,0 ,0 ) to the poin t D (1,1,0) on t h e z = 0 plane along the paths OABD as shown in the figure (where the coordinates are measured in meters) is,
If 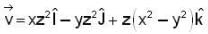 then calculate the flux of
then calculate the flux of 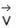 out of the region through the surface at z = c where region is bounded by -a ≤ x ≤ a, - b ≤ y ≤ b
out of the region through the surface at z = c where region is bounded by -a ≤ x ≤ a, - b ≤ y ≤ b
The circulation of the field 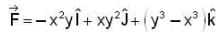 around the curve C where C is the intersection of the sphere x2+ y2 + z2 = 25 and the plane z = 3, is,
around the curve C where C is the intersection of the sphere x2+ y2 + z2 = 25 and the plane z = 3, is,
Let 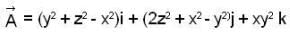 be a vector point function and S be an open surface x2 + y2 - 4x + 4z = 0 , z ≥ 0, Then the value of
be a vector point function and S be an open surface x2 + y2 - 4x + 4z = 0 , z ≥ 0, Then the value of 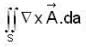 is equal to
is equal to
Let 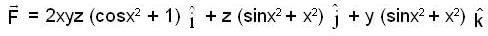 and
and 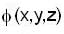 be a scalar function which satisfy Laplace eqn. Then the vector field
be a scalar function which satisfy Laplace eqn. Then the vector field 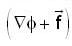 is _______.
is _______.
Let 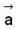 be a constant vector and
be a constant vector and 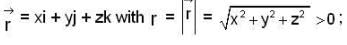 then
then 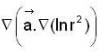 is equal to
is equal to
If 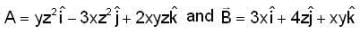 then the value of
then the value of 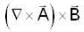 at the point (-1, 1, 1) is
at the point (-1, 1, 1) is
Let  is a unit vector, then for the maximum value of the scalar triple product
is a unit vector, then for the maximum value of the scalar triple product  will be equal to ?
will be equal to ?
Let there be two points A and B on the curve y = x2 in the plane OXY satisfying  then length of the vector
then length of the vector 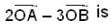
Find equations for the tangent plane to the surface z = x2 + y2 at the point (2, -1, 5).


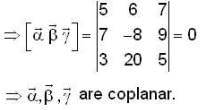
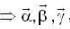 None o f vector be the Scalar multiple of other.
None o f vector be the Scalar multiple of other.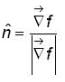
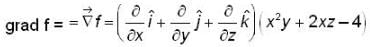
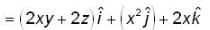
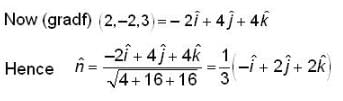

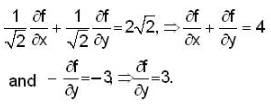
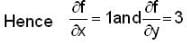
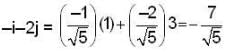

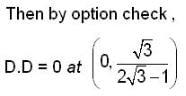
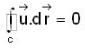 and we know that if the line integral is zero then given curve c is closed.
and we know that if the line integral is zero then given curve c is closed.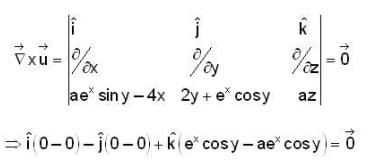
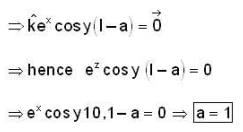
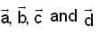 are coplanar vector’s then
are coplanar vector’s then 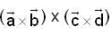 is equal to?
is equal to?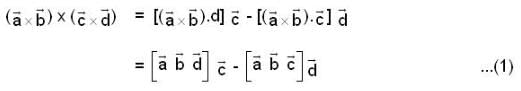
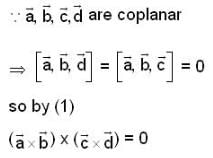
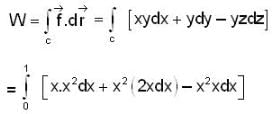
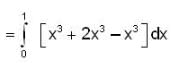
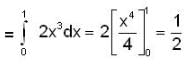
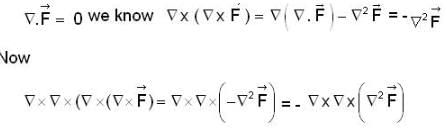
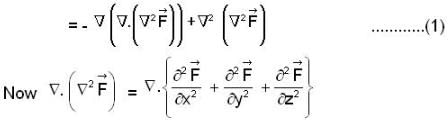
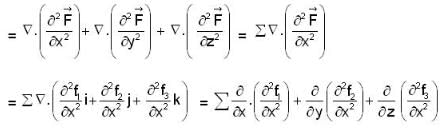
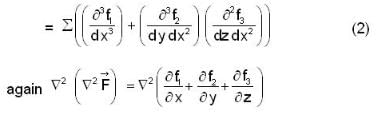
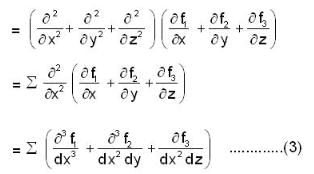
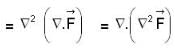
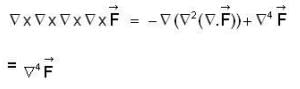
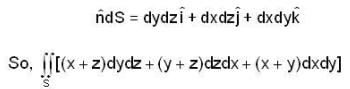
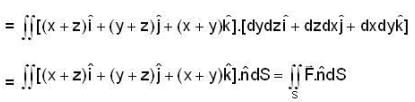
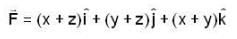
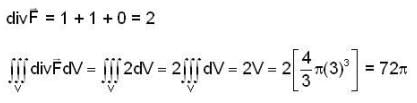

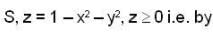
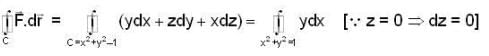
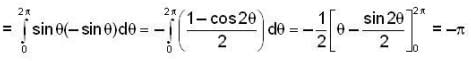
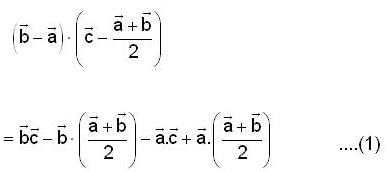
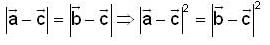

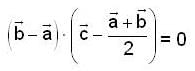
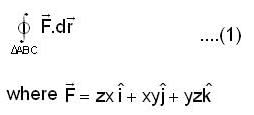
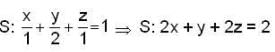
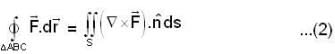
 is outward going UNV to S and given by
is outward going UNV to S and given by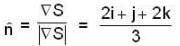
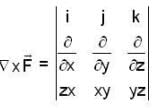
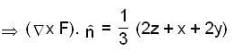

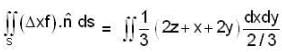
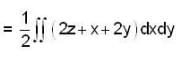
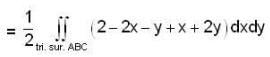
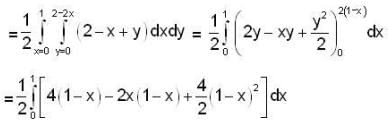
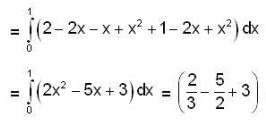
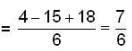
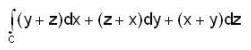
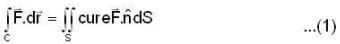
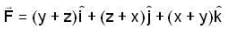
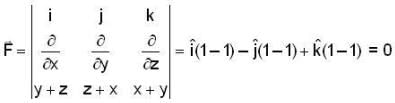
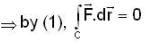
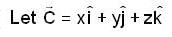
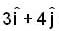 is
is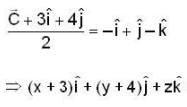
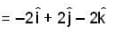
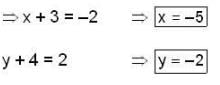
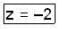
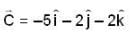
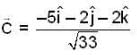
 are
are are orthogonal then
are orthogonal then 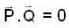
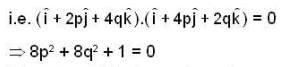
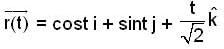
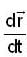 will a tangent vector
will a tangent vector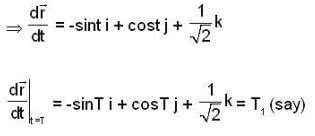
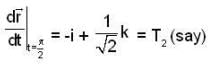

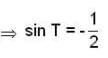
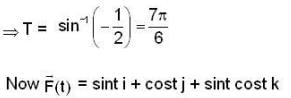
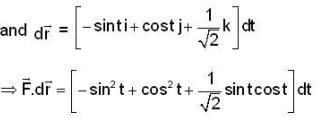

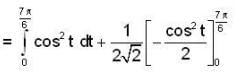
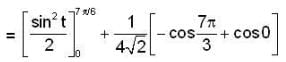
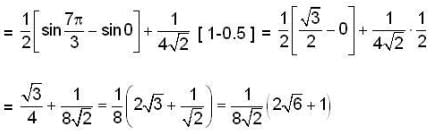
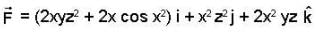
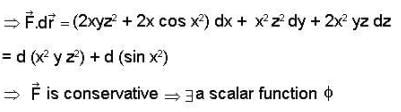
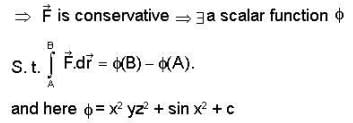

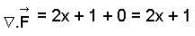
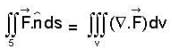
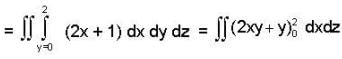
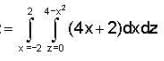
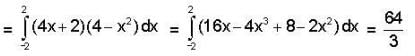
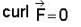
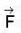 is conservative vector field.
is conservative vector field. 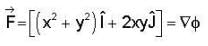
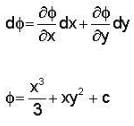
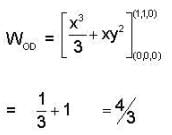
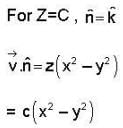

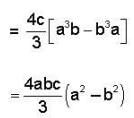

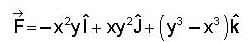
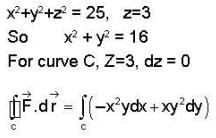

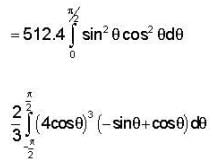
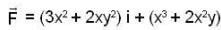 j and let L be the curve
j and let L be the curve 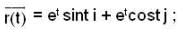
 is equal to
is equal to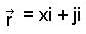 be the position vector of any point on L (in Cartesian from)
be the position vector of any point on L (in Cartesian from) 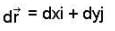
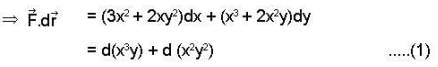
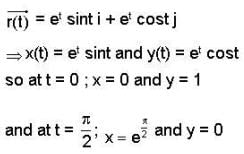

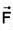 is conservative so
is conservative so 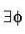
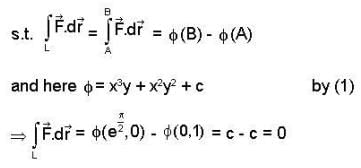
 now S be an open surface so we will use stoke’s theorem here.
now S be an open surface so we will use stoke’s theorem here. 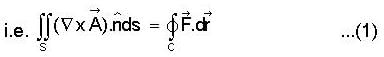
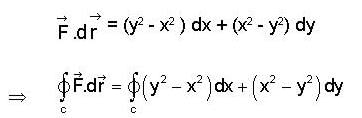
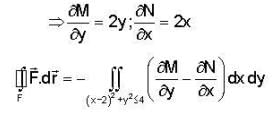
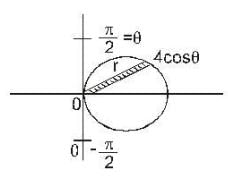
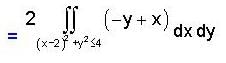
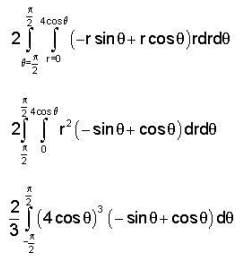
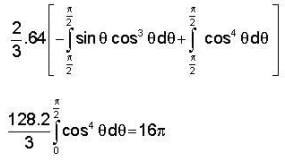
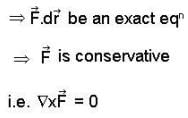
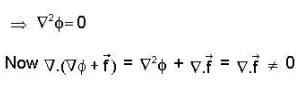
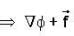 not a solenoidal vector field.
not a solenoidal vector field.
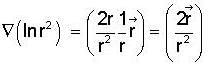
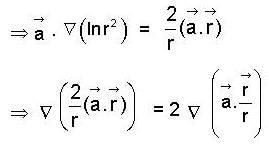

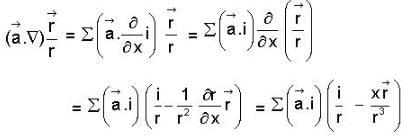
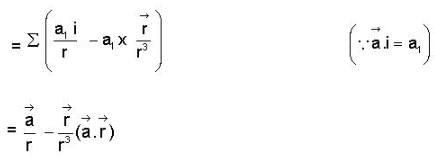
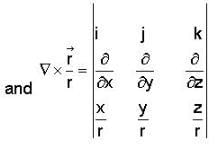
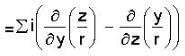
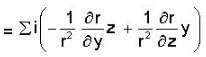
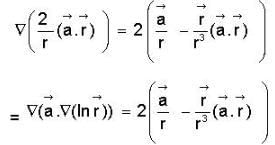
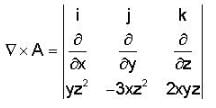
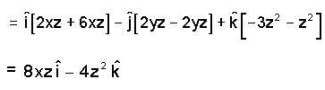

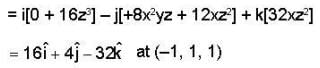
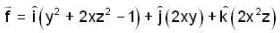 then f is
then f is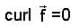
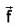
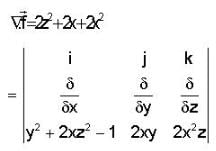
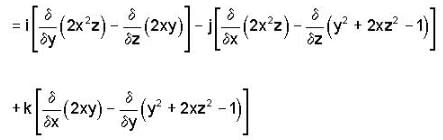
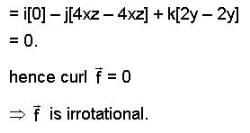
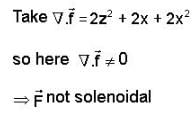
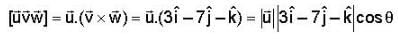

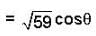
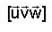 is maximum if cos θ = 1 i.e. θ = 0°
is maximum if cos θ = 1 i.e. θ = 0°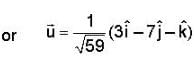
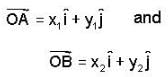
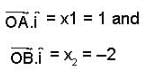

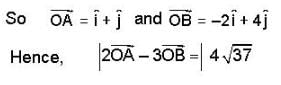
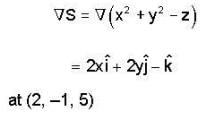
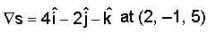 (1)
(1) ⇒ 4(x - 2) - 2(y + 1) - 1 (z - 5) = 0
⇒ 4(x - 2) - 2(y + 1) - 1 (z - 5) = 0










