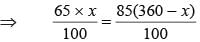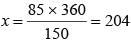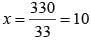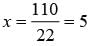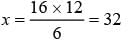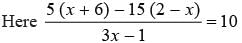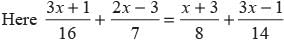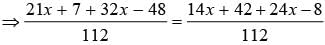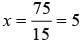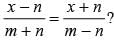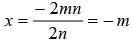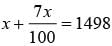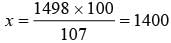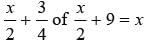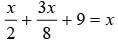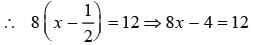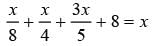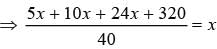Olympiad Test: Linear Equations In One Variable - Grade 10 MCQ
20 Questions MCQ Test - Olympiad Test: Linear Equations In One Variable
A boat goes downstream and covers the distance between two ports in 4 hours, while it covers the same distance upstream in 5 hours. If the speed of the stream is 2km/hour. what is the speed of boat in still water ?
The ages of Mohan and Sohan are in the ratio 9 : 7. Ten years ago their ages were in the ratio 7 : 5. What is the difference between their present ages?
The sum of two numbers is 360. If 65% of one number is equal to 85% of the other. What is the largest number among them?
A certain number of workers can finish a piece of work in 70 days. If there are 20 men less, it would take 10 days more for the same work to be finished. How many workers were there in starting?
The sum of three consecutive multiples of 11 is 363. Which of these multiple is greatest?
Arun’s age is three times his son’s age. 10 years age he was 5 times his son’s age. What is the sum of their present ages?
Nirmal thinks of a number and subtracts 5/2 from it. He multiplies the result by 8. The result now obtained is 3 times the same number he thought of. Find the number.
The difference between the digits of a two-digit number is 3. If the digits are interchanged and the resulting number is added to the original number we get 143. What was the original number?
A grand father is ten times older than his grandson. He is then also 54 years older than him. What is the difference of their present ages?
An altitude of a triangle is five-thirds the length of its corresponding base. If the altitude is increased by 4 cm and the base is decreased by 2 cm, but the area of triangle remains the same. Find the base and altitude of the triangle respectively.
A field can be ploughed in 18 days. If everyday an additional area of 16 hectares is ploughed, the field can be ploughed in 12 days. What is the area of the field?
The sum of the digits of a two number is 9. If 9 is subtracted from the number its digits are interchanged. What is the number?
What is the value of x in the given equatiom?
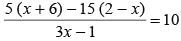
What is the value of x in the given equation
A shirt is sold for Rs. 1498 and the seller gains 7% on it. What is the cost price of the shirt ?
Half of a herd of deer are grazing in the field and three fourth of remaining are playing nearby. The rest nine are drinking water from the river. What is the number of deer in the herd?
The ages of Raju and Rajan are in the ratio 5 : 8. If Raju was 5 years older and Rajan 4 years younger, the age of Raju would have been the same as the age of Rajan. What is the age of Raju?
If 1/2 is subtracted from a number and the difference is multiplied by 8, the result is 12. What is the number?
Mohaesh travelled 1/8 th of his Journey by bus, 1/4 th by taxi, 3/5 th by train and remaining 8 km by foot. What is the length of his total Journey?