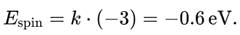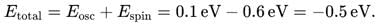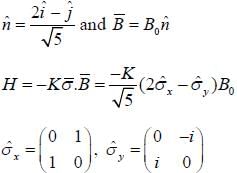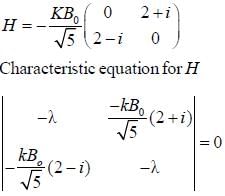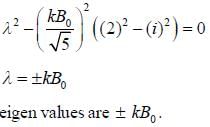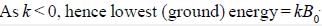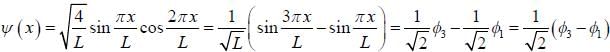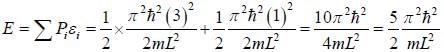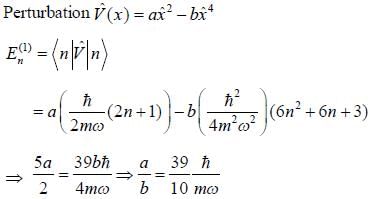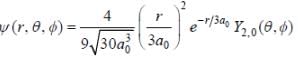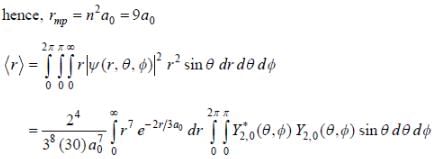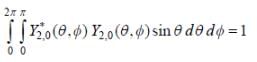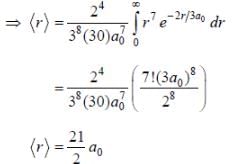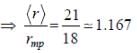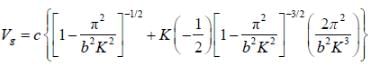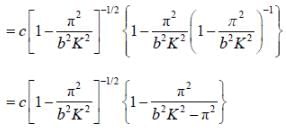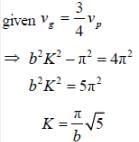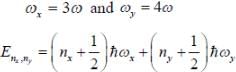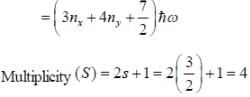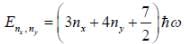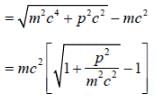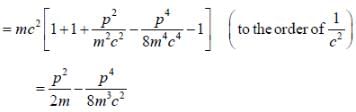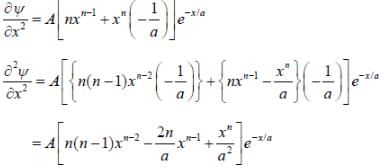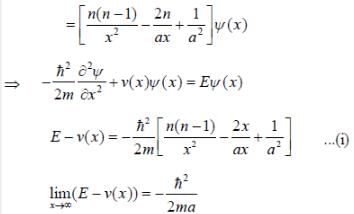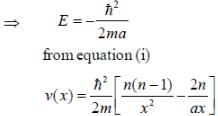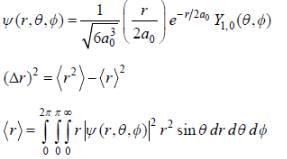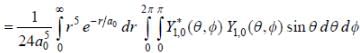Test: Quantum Mechanics - 2 - Physics MCQ
20 Questions MCQ Test - Test: Quantum Mechanics - 2
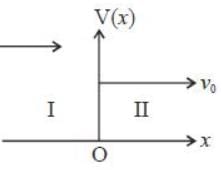
An electron with energy 'E' is coming from far left to a potnetial step at x = 0. If E/V =9/8 then ratio of wavelength (λ1/λ2) of electron in region I and II is (Upto two decimal places)

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Wavefunction of a particle iii some one dimension potential is given by,
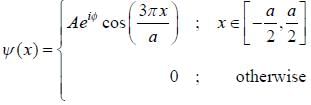
where k is the positive real constant. Probability of:finding the particle between x = 0 and x = a/4 is _____ %. (Upto two decimal places)
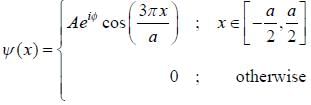
where k is the positive real constant. Probability of:finding the particle between x = 0 and x = a/4 is _____ %. (Upto two decimal places)
Consider the spin state of a system in 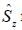 reresentation
reresentation
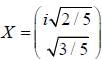
What is the average value of the operator 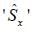 corresponding to the x-component of the spin.
corresponding to the x-component of the spin.
Find the eigenvalues of the component of spin operator 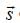 of an electron in direction of a unit vector with spherical coordinates
of an electron in direction of a unit vector with spherical coordinates 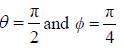
An operator 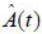 operates on a state vector such that
operates on a state vector such that 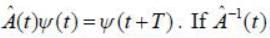 is known to be existed, then
is known to be existed, then 
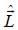 represent the total angular momentum operator. The value of
represent the total angular momentum operator. The value of 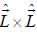 is
is
A particle of mass m is being scattered by a potential given by V(r) = 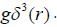 The differential cross-section calculated by Born's approximation is
The differential cross-section calculated by Born's approximation is
Consider a particle in the 1-D potential well given by
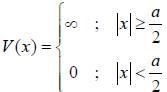
Now, a small perturbation is added to the well given as
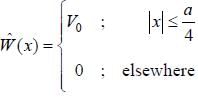
The first-order correction to the energy of second energy level, is
In a two-dimensional vector space spanned by basis vectors 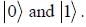 Two vectors in this space are given as
Two vectors in this space are given as

An operator 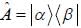 is represented by matrix.
is represented by matrix.
An electron is placed in an uniform magnetic field 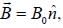 where
where 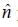 points in the direction of vector
points in the direction of vector 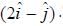 The Hamiltonian of the system is H =
The Hamiltonian of the system is H = 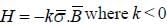 is a constant and
is a constant and 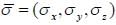 are pauli matrices Energy of ground state in terms of kB0
are pauli matrices Energy of ground state in terms of kB0
A particle of mass 'm' with in box of length L, the wave function of the state is given by

then the energy of the particle of the state is
A linear harmonic oscillator is perturbed by the potential V' (x) = ax2-bx4; a and b constants. If first order energy correction to the second excited energy level is zero then 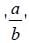 in units of
in units of 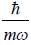 is (Upto two decimal places)
is (Upto two decimal places)
The wave function of a hydrogen atom is given by 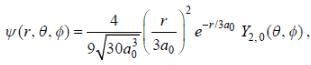 where 'a0' is Bohr radius and
where 'a0' is Bohr radius and  is spherical harmonic function for l = 2 and m = 0. If probability of finding the electron is maximum at 'rmp' and average distance between electron and proton is <r> then ratio of the two
is spherical harmonic function for l = 2 and m = 0. If probability of finding the electron is maximum at 'rmp' and average distance between electron and proton is <r> then ratio of the two 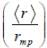 is (upto two decimal places)
is (upto two decimal places)
Angular frequency for a wave propagating inside a waveguide is given in terms of the wave number K and the width of the guide b as
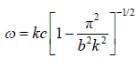
If group velocity is 3/4th of the velocity then k is
Seven spin -3/2 identical non-interacting particle are subjected to the potential given as
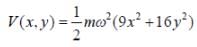
The lowest energy of the system is
A particle of mass 'm' in 1-D harmonic oscillator potential  In the non-relativistic limit, where the kinetic energy T and momentum P are related as T = p2/2m. The ground state energy is known to be
In the non-relativistic limit, where the kinetic energy T and momentum P are related as T = p2/2m. The ground state energy is known to be 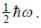 For the relativestic corrections in relation between T and P, calculate energy shift in ground state to the order of 1/c2 (c is speed of light in vacuum)
For the relativestic corrections in relation between T and P, calculate energy shift in ground state to the order of 1/c2 (c is speed of light in vacuum)
The wave function of a one-dimensional system is given as
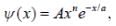
where A, n and a are positive constants. The form of the potential if V(x) → 0 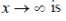
The wavefunction of a hydrogen atom is given by
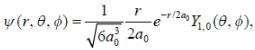
where a0 is Bohr radius and 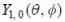 is spherical harmonic function for l = 1 and m = 0. What is the dispersion in the measurement of distance of electron from nucleus?
is spherical harmonic function for l = 1 and m = 0. What is the dispersion in the measurement of distance of electron from nucleus?




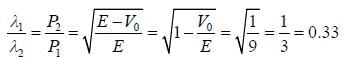
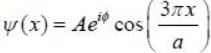
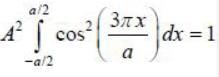
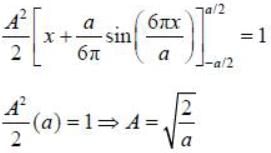
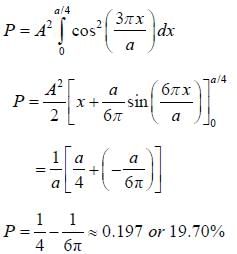
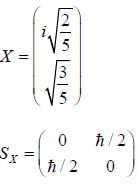
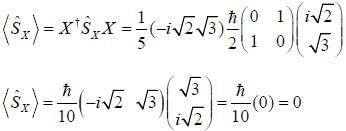
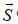 do not depent on direction
do not depent on direction 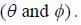 They are always
They are always 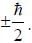
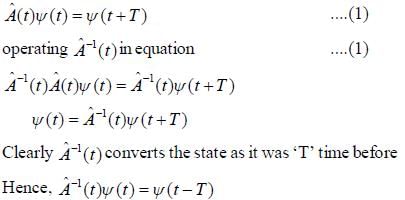

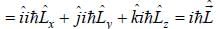
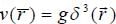
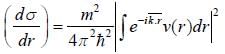
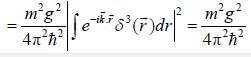
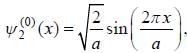
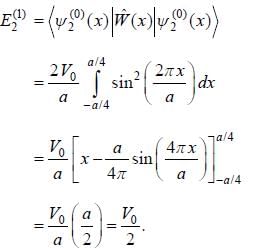
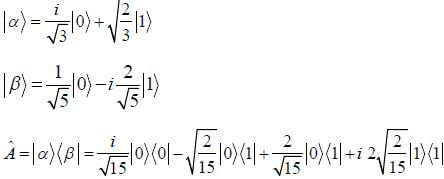
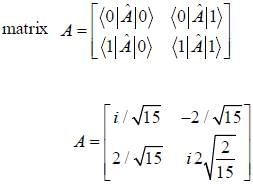
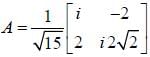
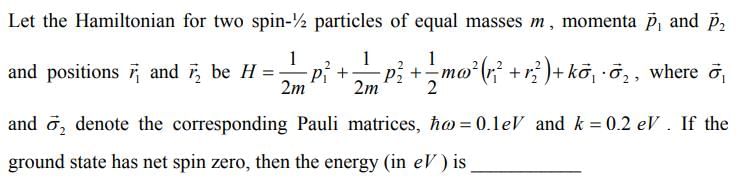
 describes the spin-spin interaction.
describes the spin-spin interaction.
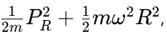
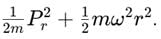
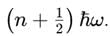 For the ground state (n=0), the total harmonic oscillator energy is:
For the ground state (n=0), the total harmonic oscillator energy is: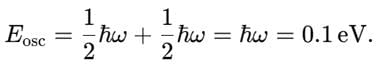
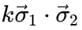 depends on the relative spin orientation:
depends on the relative spin orientation: