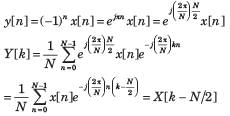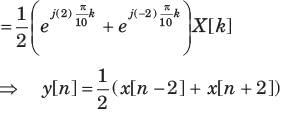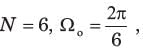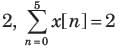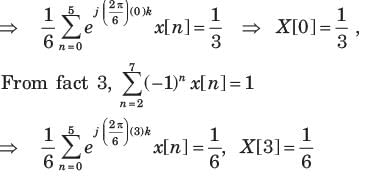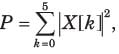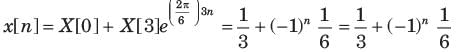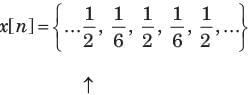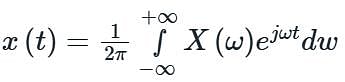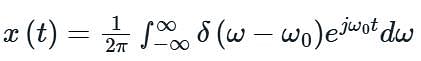Test: Fourier - 3 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Fourier - 3
Consider a periodic signal x[n] with period N and FS coefficients X [k]. Determine the FS coefficients Y [k] of the signal y[n] given in question.
Q. y[n] = (-1)n x[n], (assume that N is even)
Q. y[n] = (-1)n x[n], (assume that N is even)
Consider a discrete-time periodic signal
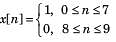
Also a function y[n] is defined as y[n] = x[n] - x[n - 1]
Q. The fundamental period of y[n] is
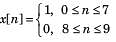
Also a function y[n] is defined as y[n] = x[n] - x[n - 1]
Q. The fundamental period of y[n] is
Consider a discrete-time signal with Fourier representation.
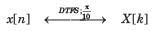
In question the FS coefficient Y [k] is given. Determine the corresponding signal y[n] and choose correct option.
Q. Y [k] = X[k - 5] + X[k + 5]
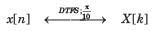
In question the FS coefficient Y [k] is given. Determine the corresponding signal y[n] and choose correct option.
Q. Y [k] = X[k - 5] + X[k + 5]
Consider a discrete-time signal with Fourier representation.
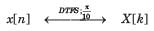
In question the FS coefficient Y [k] is given. Determine the corresponding signal y[n] and choose correct option.
Q. Y [k] = cos (πk/5)X[k]
Consider a discrete-time signal with Fourier representation.
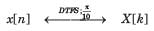
In question the FS coefficient Y [k] is given. Determine the corresponding signal y[n] and choose correct option.
Q. Y [ k] = X [k] * X [k]
Consider a discrete-time signal with Fourier representation.
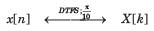
In question the FS coefficient Y [k] is given. Determine the corresponding signal y[n] and choose correct option.
Q. Y [k] = Re{ X [ k]}
Consider a sequence x[n] with following facts :
1. x[n] is periodic with N = 6
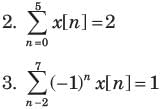
4. x[n] has the minimum power per period among the set of signals satisfying the preceding three condition.
The sequence would be.
A real and odd periodic signal x[n] has fundamental period N = 7 and FS coefficients X [k]. Given that X [15] = j, X [16] = 2j, X [17] = 3j. The values of X [0],X [ -1], X [-2 ], and X [-3] will be
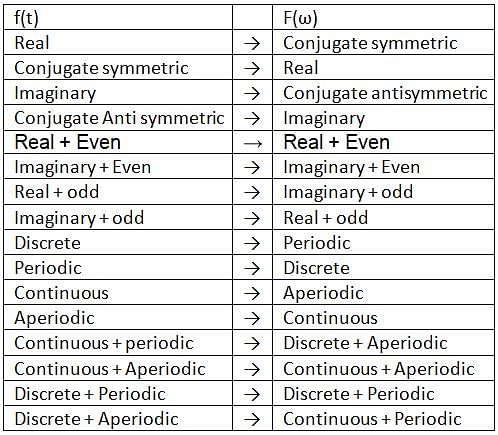
In the Fourier transform, if the time domain signal x(t) is real and even, then the frequency domain signal X(jΩ) will be: