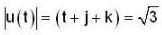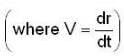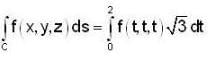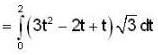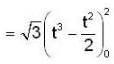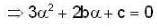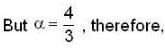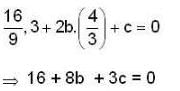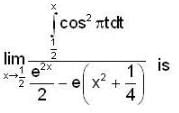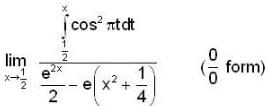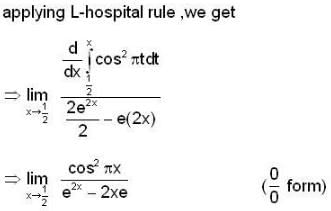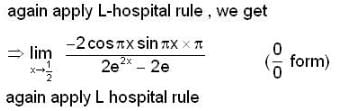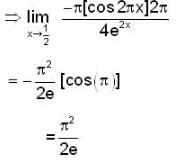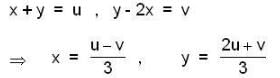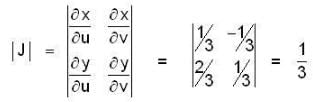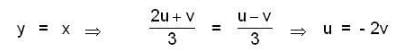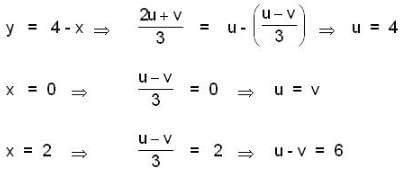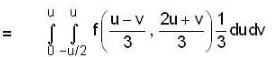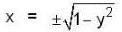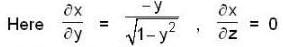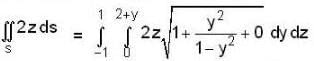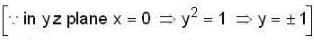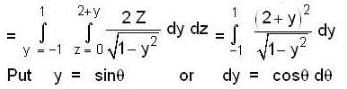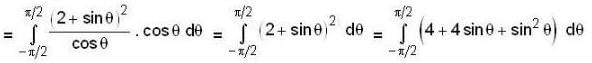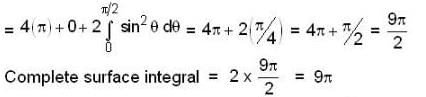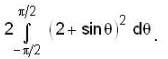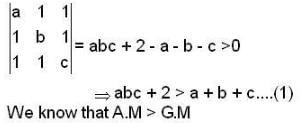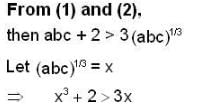IIT JAM Mathematics Practice Test- 20 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 20
If f(x) = (x2 - 1) |x2 - 3x + 2| + cos|x| then the set of point of non-differentiability is,
If we expand sin x by Taylor’s series about π/2, then a2,a7,a4,a3 are,
If f(x + y) = f(x) + f(y) , and f(x) is differentiable at one point of R, then f(x) is.
and f(x) is differentiable at one point of R, then f(x) is.
 and f(x) is differentiable at one point of R, then f(x) is.
and f(x) is differentiable at one point of R, then f(x) is.Let A and B be non-empty subsets of real line R, which of the following statement would be equivalent to sup A < in fB ?
Let V be a vector space and T transformation from V to V. then the intersection of the range of T and the null space of T is the zero subspace from of V if and only if.
Let F : R3 → R2 be a linear mapping defined by f(x,y,z) = (3x + 2y - 4z, x - 5y + 3z). then the matrix of F relative to the basis {(1,1,1),(1,1,0),(1,0,0)} and {(1,3),(2,5)} is,
Consider the matrix  then the eigenvalues of matrix B = A2 + 2A + I are,
then the eigenvalues of matrix B = A2 + 2A + I are,
Let X be a proper closed subset of [0,1]. Which of the following statements is always true ?
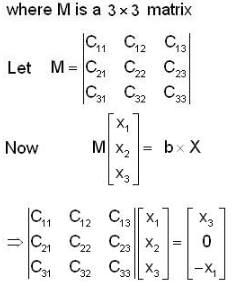
The linear operation L(x) is defined by the cross product L(x) = bX, where b = [0 1 0]T and x = [x1 x2 x3]T are three dimensional vectors. The 3 x 3 matrix M of this operation satisfies 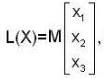 then the eigenvalues of M are
then the eigenvalues of M are
Differentiation of function f(x, y, z) = Sin(x)Sin(y)Sin(z) - Cos(x) Cos(y) Cos(z) w.r.t ‘y’ is?
How many numbers satisfied the equation x ≌ 7 (mod 17), where x in the range 1 < x < 100.
The value of 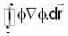 for closed curve C is equal to
for closed curve C is equal to
Which of the following is a 2 -dimensional subspace of R3 over R ?
Let P(x) be a vector space of all real polynomials with degree < n and w be a subset of V, given as 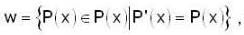 Then dim ension of w is
Then dim ension of w is
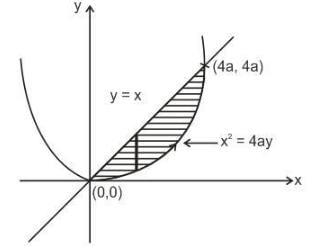
The value of the line integral 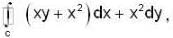 where C is the closed curve of the region bounded by y = x and x2 = 4ay is
where C is the closed curve of the region bounded by y = x and x2 = 4ay is
If sn denotes the permutation group and (12) ∈ s5 then determine all elements in s5. which commute with (12).
The line integral 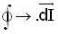 of a vector field
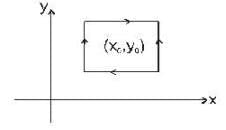
of a vector field 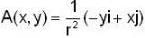 where r2 = x2 + y2 is taken around a square (as shown in the figure) of side unit length and centered at
where r2 = x2 + y2 is taken around a square (as shown in the figure) of side unit length and centered at 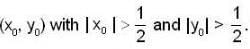 If the value of the integral is L, then
If the value of the integral is L, then
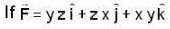 and S is that part of the surface of the sphere x2 + y2 + z2 = 1, which lies in the first octant then the value of
and S is that part of the surface of the sphere x2 + y2 + z2 = 1, which lies in the first octant then the value of 
The value of line integral  where path is given in the figure and f(x,y,z) = 3x2 - 2y + z,
where path is given in the figure and f(x,y,z) = 3x2 - 2y + z,
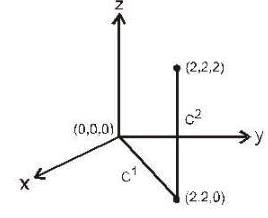
The value of line integral 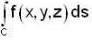 , where C is the line segment joining the origin to the point (2, 2, 2) and f(x, y, z) = 3x2 = 2y + z is
, where C is the line segment joining the origin to the point (2, 2, 2) and f(x, y, z) = 3x2 = 2y + z is
Rolle’s theorem holds for the function x3 + bx2 + cx , 1 < x < 2 at the point 4/3, then the value of b and c are
Let G be a group of order 143, then the centre of G is isomorphic to
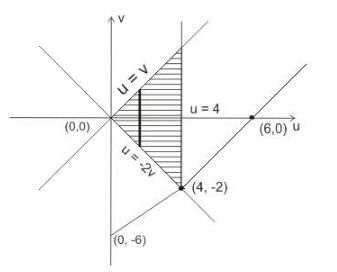
The double integral 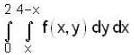 under the transformation u = x + y , v = y - 2x is transformed into
under the transformation u = x + y , v = y - 2x is transformed into
Let S be the bounded surface of the cylinder x2 + y2 = 1 cut by the planes z = 0 and z = 2 + y, then the value of the surface integral 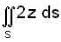 is equal to
is equal to
If the value of the determinant 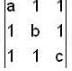 is positive then,
is positive then,


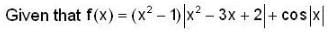
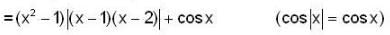
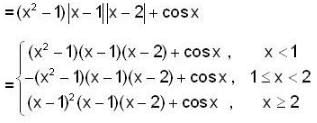
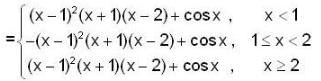
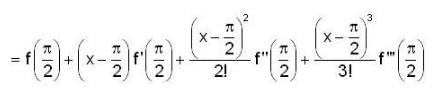
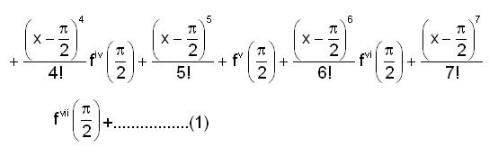
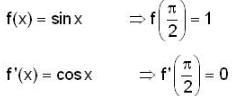


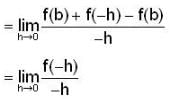
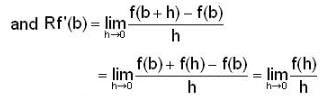

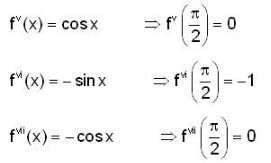
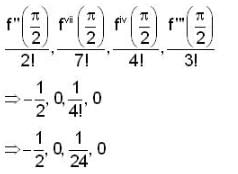
 then the value of
then the value of 
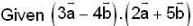
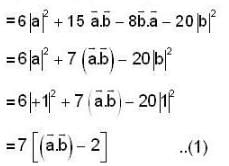
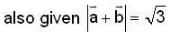
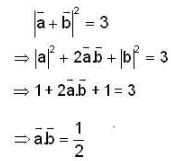
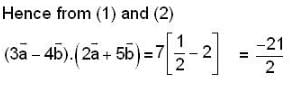
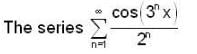
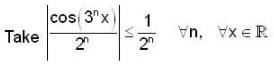
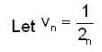
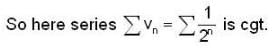

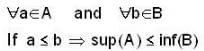
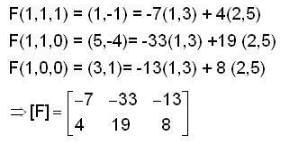
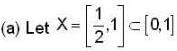 proper closed subset of [0,1] but X not countable
proper closed subset of [0,1] but X not countable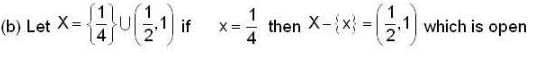
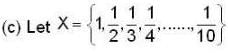 be a proper closed subset of [0,1] but it cannot contain an open interval.
be a proper closed subset of [0,1] but it cannot contain an open interval.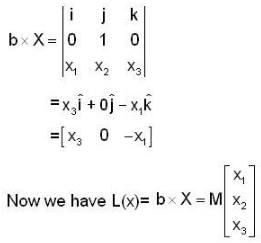
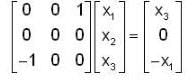
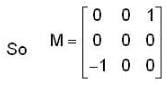
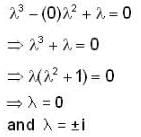
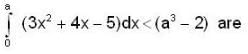
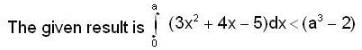
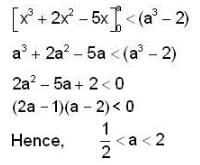
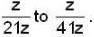
 be a homomorphism then in general, there are d
be a homomorphism then in general, there are d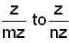 where d = g.c.d(m,n).
where d = g.c.d(m,n).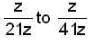
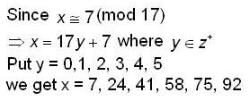
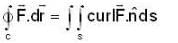
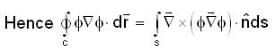
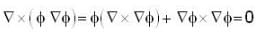

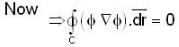
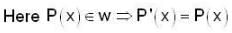
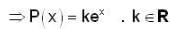
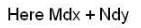
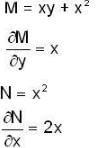
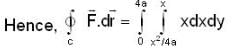
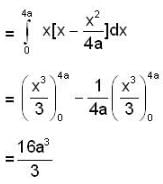

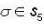 is clearly (n-2)l
is clearly (n-2)l will take remaining (n-2) letters among themselves and so σ will be a permutation on (n-2) letters]
will take remaining (n-2) letters among themselves and so σ will be a permutation on (n-2) letters]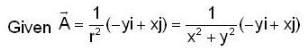
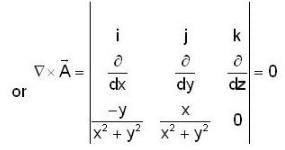
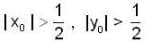
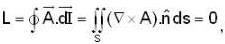 which is independent of (X0, y0)
which is independent of (X0, y0)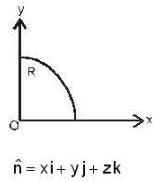
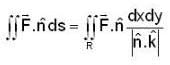
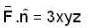
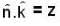
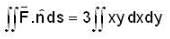
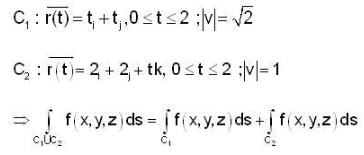
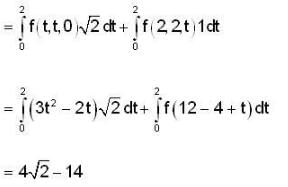
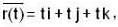 where 0 < t < 2. The component have continuous 1st order derivative and
where 0 < t < 2. The component have continuous 1st order derivative and