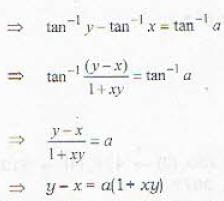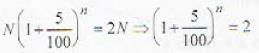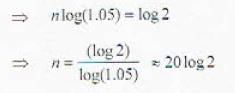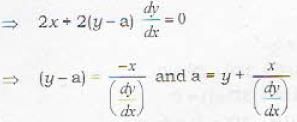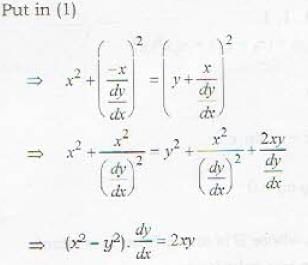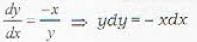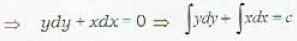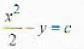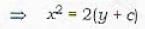Differential Equations - 13 - Mathematics MCQ
20 Questions MCQ Test - Differential Equations - 13
The function f defined by f(x) - x [1 + 1/3 sin (log x2)], a ≠ 0,/(0) = 0 ([] represents the greatest integer function) is
If f is twice differentiable function such that f ''(x) = - f(x), f '(x) = g(x) and h(x) = [f(x)]2 + [g(x)]2, also if h(5) = 11, then h(10) is equal to
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The solution of the differential equation y(2xy + ex)dx - exdy = 0 is
The half-life of a radioactive substance is the time required for one-half of that substance to decay. The amount of 11C, an isotope of carbon present at a future time t (in months) is given by A(t) = 100 exp [- 0.0338 t]. The half life of the material in months is
Consider a pair of differential equations 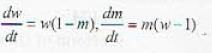
Eliminating t in the two equations results in
The rare at which body changes temperature is proportional to the difference between its temperature and ihat of the surrounding medium. This is called Newton's law of cooling. If y = f{t} is the unknown temperature of The body at time t and M(t) denotes the known temperature of the surrounding medium, Newton's law' leads to the differential equation where k is a positive constant.
tan-1 x + tan-1 y = c is the general solution of the differential equation
The solution of the differential equal ion (1 + x2) dy/dx = (1 + y2) is
If a population grows at the rate of 5% per year, it will double (in years) after
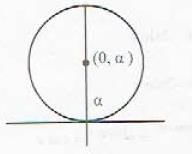
The differential equation of all circles passing through the origin and having their centres on the y-axis is
The geometrical interpretation of the graph of the differential equation: 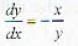 is a family of
is a family of
The solution curves of the given differential equation: xdx - dy = 0 constitute a family of
If left to grow undisturbed, the fish population in a lake would be 50 per cent more than it was in the previous year. However, for research purposes 100 fishes are added to the population each year. If the initial population of fish in the pond was zero then how many years the slocking program should continue till the population increases to 2000?


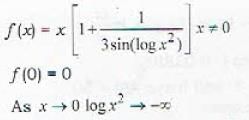
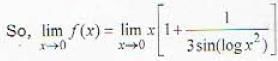
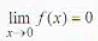 due to factor x in it.
due to factor x in it.
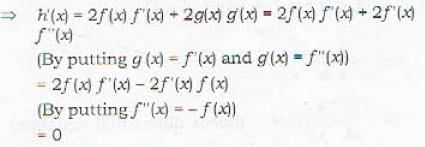
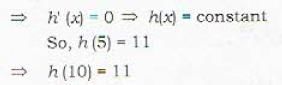

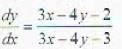 ........(i)
........(i)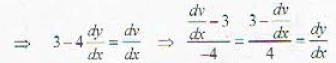
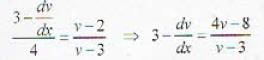

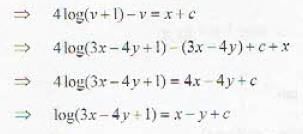
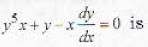
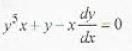
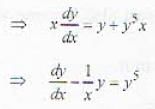
 .....(i)
.....(i)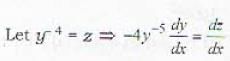
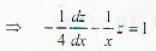
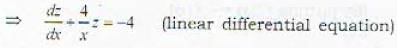

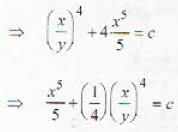

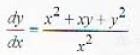 ....(i)
....(i)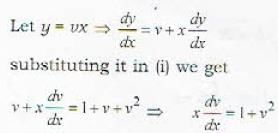
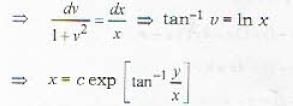
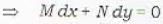
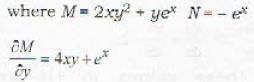
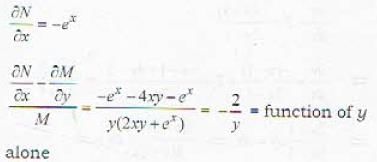
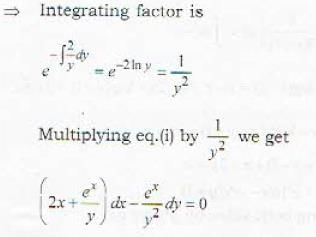



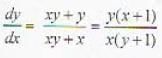
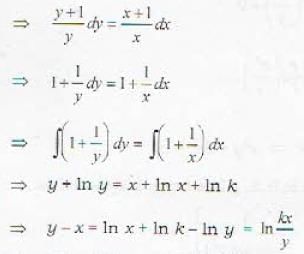
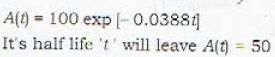
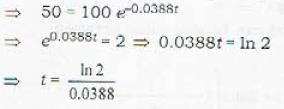
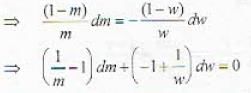
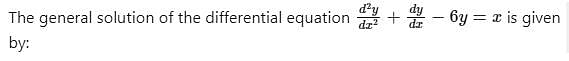


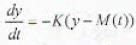
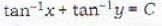
 (By differentiating)
(By differentiating)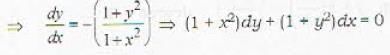
 represents
represents
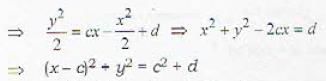
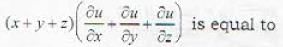
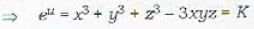
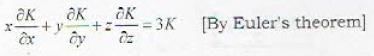
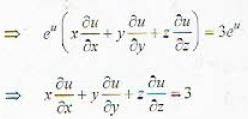

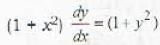
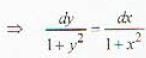 ......(i)
......(i)