Test: Miscellaneous Topics- 1 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test - Test: Miscellaneous Topics- 1
If a node has K children in B tree, then the node contains exactly keys.
The time complexity of the following C function is, (assume n> 0)
int recursive (int n )
{ if ( n = = 1)
return (1);
else
return (recursive ( n - 1) + recursive ( n - 1));
}
int recursive (int n )
{ if ( n = = 1)
return (1);
else
return (recursive ( n - 1) + recursive ( n - 1));
}
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The number of spanning trees for a complete graph with seven vertices is
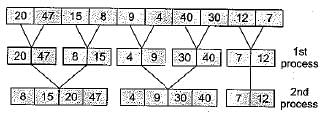
if one uses straight two-way merge sort algorithm to sort the following elements in ascending order:
20, 47, 15, 8, 9, 4, 40, 30, 12, 17
Then the order of these elements after second pass of the algorithm is
Consider the following sorting algorithms:
1. Quicksort
2. Heapsort
3. Mergesort
Which of them perform in least time in the worst case?
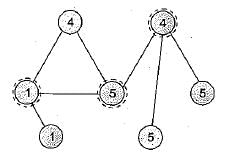
The number of articulation points of the following graph is:
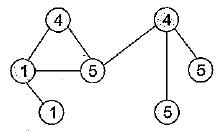
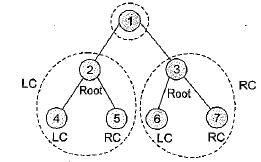
Consider the following tree:
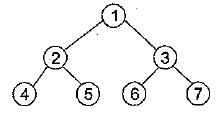
If the post order traversal gives ab - cd* + then the label of the nodes 1,2, 3, ... will be
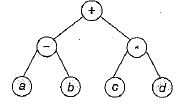
The expression tree given in figure evaluates to 1, if
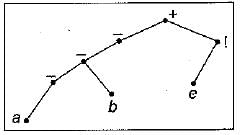
1. a = - b and e = 0
2. a = - b and e = 1
3. a = b and e = 0
4. a = b and e = 1
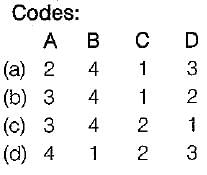
Match List-I with List-ll and select the correct answer using the codes given beiow the lists:
List-I
A. All pairs shortest path
B. Quick sort
C. Minimum weight spanning tree
D. Connected Components
List-ll
1. Greedy
2. Depth-first search
3. Dynamic programming
4. Divide and conquer
Consider the following tree:

If this tree is used for sorting, then a new number 8 should be place as the