Test: Dynamic Programming, P & NP Concepts- 2 - Computer Science Engineering (CSE) MCQ
5 Questions MCQ Test - Test: Dynamic Programming, P & NP Concepts- 2
What is the time complexity of Bellman-Ford single-source shortest path algorithm on a complete graph of n vertices?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which of the following statements are TRUE?
1. The problem of determining whether there exists a cycle in an undirected graph is in P.
2. The problem of determining whether there , exists a cycle in an undirected graph is in NP.
3. If a problem A is NP-Complete, there exists a non-deterministic polynomial time algorithm to solve A
1. The problem of determining whether there exists a cycle in an undirected graph is in P.
2. The problem of determining whether there , exists a cycle in an undirected graph is in NP.
3. If a problem A is NP-Complete, there exists a non-deterministic polynomial time algorithm to solve A
Consider two decision problems Q1, Q2 such that Q1 reduces in polynomial time to 3-SAT and 3-SAT reduces in polynomial time to Q2. Then which one of the following is consistent with the above statement?
Language L1 is polynomial time reducible to language L2. Language L3 is polynomial time reducible to L2, which in turn is polynomial time reducible to language L4. Which of the following is/are True?
I. If L4 ∈ P , L2 ∈ P
II If L, ∈ P or L3e P, then L2∈ P
III. L, ∈ P, if and only if L3∈ P
IV. If L4 ∈ P, then L1 ∈ P and L3 ∈ P


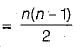
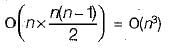
 so this problem will also be considered as NP problem.
so this problem will also be considered as NP problem. is NP-problem 3-SAT ≤ Q2 and 3-SAT is NP-hard ⇒ Q2 is NP- hard problem.
is NP-problem 3-SAT ≤ Q2 and 3-SAT is NP-hard ⇒ Q2 is NP- hard problem.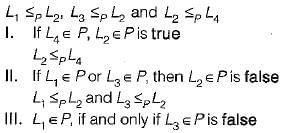
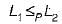
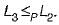
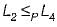 we can get that L2∈ P.
we can get that L2∈ P.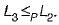 we can now get that L3 ∈ P
we can now get that L3 ∈ P 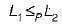 we can get that L1 ∈ P
we can get that L1 ∈ P














