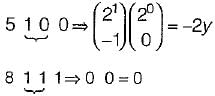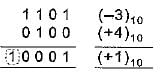Test: Floating Point Number- 2 - Computer Science Engineering (CSE) MCQ
12 Questions MCQ Test - Test: Floating Point Number- 2
For interval arithmetic best rounding technique use is ________.
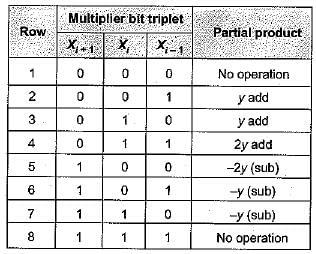
When multiplicand Y is multiplied by multiplier X = xn-1xn-2 ... x0 using bit- pair recording in Booth’s algorithm, partial products are generated according to the following table:
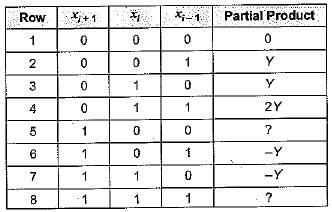
Q. The partial products for rows 5 and 8 are

Consider the following floating point format:
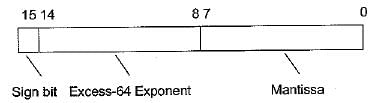
Mantissa is a pure fraction is sign-magnitude form.
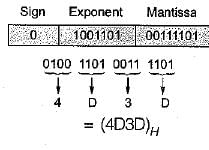
Q. The decimal number 0.239 x 213 has the following hexadecimal representation without normalization and rounding off

Mantissa is a pure fraction is sign-magnitude form.
Consider the following floating point format:

Mantissa is a pure fraction is sign-magnitude form.
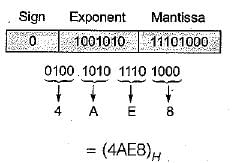
Q. The normalized representation for the above format is specified as follows. The mantissa has an implicit 1 preceding the binary (radix) point. Assume that only 0’s are padded in while shifting a field. The normalized representation of the above number (0.239 x 213) is
The addition of 4-bit, two’s complement, binary numbers 1101 and 0100 results in
The following bit pattern represents a floating point number in IEEE 754 single precision format:
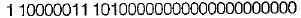
The value of the number in decimal form is
In the IEEE floating point representation the hexadecimal value 0x00000000 corresponds to
The two numbers given below are multiplied using the Booth’s algorithm.
Multiplicand: 0101101011101110
Multiplier: 0111011110111101
Q. How many additions/Subtractions are required for the multiplication of the above two numbers?
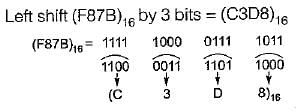
P is a 16-bit signed integer. The 2’s complement representation of P is (F87B)16. The 2's complement representation of 8*P is
The smallest integer that can be represent by and 8-bit number in 2’s complement form is
The n-bit fixed-point representation of an unsigned real number X uses f bits for the fraction part. Let i = n - f. The range of decimal values for X in this representation is