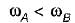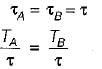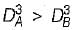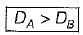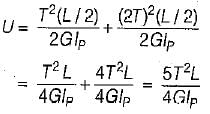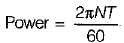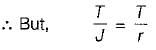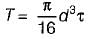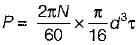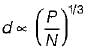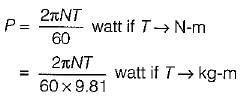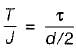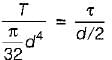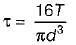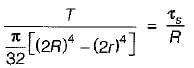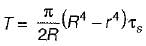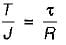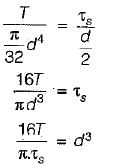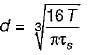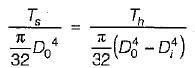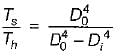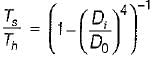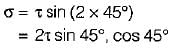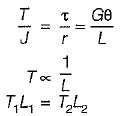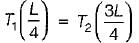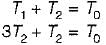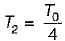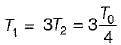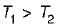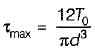Test: Torsion of Shafts - 2 - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Torsion of Shafts - 2
200 kW is to be transmitted by each of two separate shafts. A is running at 300 rpm and B at 350 rpm. Which shaft must have greater diameter?
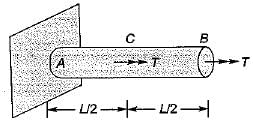
A circular bar AB of length L is fixed at end A and free at B. Torque T is acting simultaneously at B and C. What is the strain energy U stored in the bar?

For a power transmission shaft transmitting power P at N rpm, the diameter is proportional to
If a shaft is rotating at N revolutions per minute with an applied torque TN-m, the power being transmitted by the shaft in watt is
For a circular shaft of diameter d subjected to torque T, the maximum value of the shear stress is
What is the maximum torque transmitted by a hollow shaft of external radius R and internal radius r?
A solid shaft of circular cross-section is subjected to a torque T which produces a maximum shear stress τs in the shaft. The diameter of the shaft should be
The ratio of torque carrying capacity of solid shaft to that of a hollow shaft is given by
where K is ratio of inside to outside diameter?
A shaft subjected to torsion experiences a pure shear stress τ on the surface. The maximum principal stress on the surface which is at 45° to the axis will have a value of
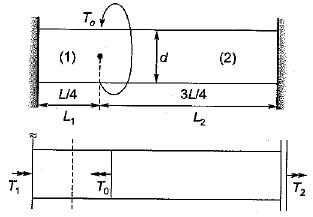
A solid shaft of diameter, d and length, L is fixed at both the ends. A torque T0 is applied at a distance L/4 from the left end as shown in figure given below.
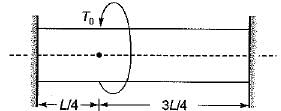
The maximum shear stress in the shaft is