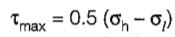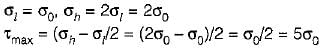Test: Thin & Thick Cylinders - 2 - Civil Engineering (CE) MCQ

A thin cylinder contains fluid at a pressure of 500 N/m², the internal diameter of the shell is 0.6 m and the tensile stress in the material is to be limited to 9000 N/m². The shell must have a minimum wall thickness of nearly

In a thick-cylinder pressurized from inside, the hoop stress is maximum at

A thick-walled hollow cylinder having outside and inside radii of 90 mm and 40 mm respectively is subjected to an external pressure of 800 MN/m². The maximum circumferential stress in the cylinder will occur at a radius of

When a thin cylinder of diameter ‘d’ and thickness ‘t' is pressurized with an internal pressure of ‘p’ (1/m is the Poisson’s ratio and E is the modulus of elasticity), then

A thin walled cyiihdrical vessel of wall thickness t and diameter d is filled with gas to a gauge pressure of p.'The maximum shear stress on the vessel wall will then be

A thin cylinder; with both ends closed is subjected to internal pressure p. The longitudinal stress at the surface has been calculated as a0. Maximum shepr ,stress at the surface will be equal to

 If a thick cylindrical shell is subjected to internal pressure, then hoop stress, radial stress and longitudinal stress at a point in the thickness will be -'mV