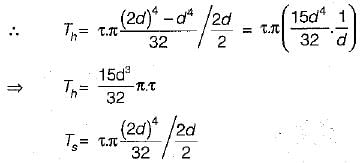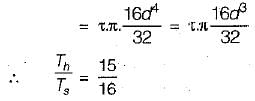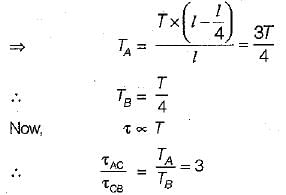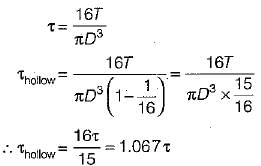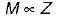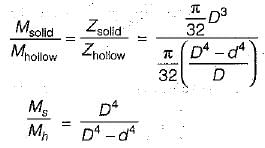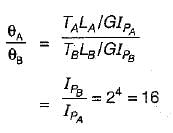Test: Torsion of Shafts - 2 - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Torsion of Shafts - 2
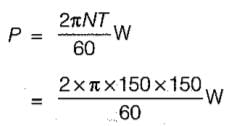
A shaft turns at 150 rpm under a torque of 150 Nm. Power transmitted is
The outside diameter of a hollow shaft is twice its inside diameter. The ratio of its torque carrying capacity to that a solid shaft of the same material and the same outside diameter is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
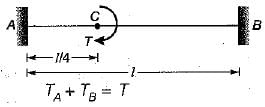
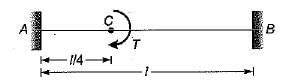
A round shaft of diameter ‘d and length T fixed at both ends A and B is subjected to a twisting moment T at C, at a distance 114 from A. The torsional stresses in the parts AC and CB will be
A solid shaft of diameter D carries a twisting moment that develops maximum shear stress τ. if the shaft is replaced by a hollow one of outside diameter ‘D’ and inside diameter D/2, then the maximum shear stress will be
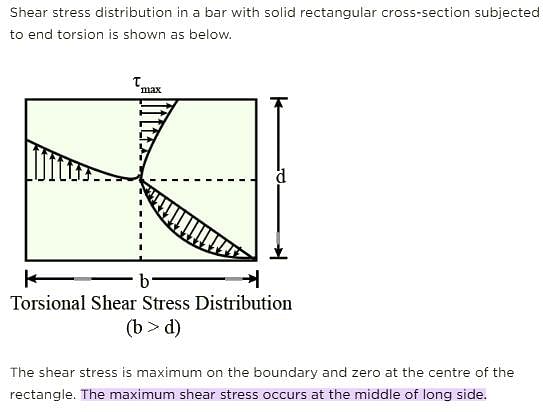
In a rectangular shaft subjected to torsion, the maximum shear occurs at
The ratio of the moment of resistance of a solid circular shaft of diameter D and a hollow shaft (external diameter D and internal diameter d) is given by
If a shaft of diameter d is subjected to a torque Tand a bending moment M, the maximum shear stress is
The diameter of shaft B is twice that of shaft A Both shafts have the same length and are of the same material, if both are subjected to same torque, then the ratio of the angle of twist of shaft' A to that of shaft B will be
If a shaft is turning at N r.p.m and the mean torque to which the shaft is subjected is T N-m, the power transmitted by the shaft in kW would be
A shaft of diameter 'd' and length L is subjected to twisting moment T, shear angle developed in shaft is 0.001 rad. Now the length of the shaft is doubled, but the diameter and torque remain the same what will be the shear angle?
Top Courses for Civil Engineering (CE)
Important Questions for Torsion of Shafts - 2
Torsion of Shafts - 2 MCQs with Answers
Online Tests for Torsion of Shafts - 2
|
© EduRev
|
Education Revolution
|
Follow Us
|
