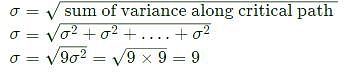Test: CPM & PERT - 2 - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: CPM & PERT - 2
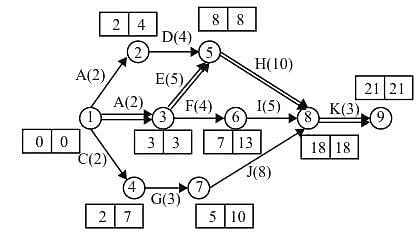
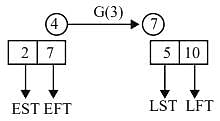
Activities A to K are required to complete a project. The time estimates and the immediate predecessors of these activities are given in the table. If the project is to be completed in the minimum possible time, the latest finish time for the activity G is _____ hours.


A PERT network has 9 activities on its critical path. The standard deviation of each activity on the critical path is 3. The standard deviation of the critical path is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
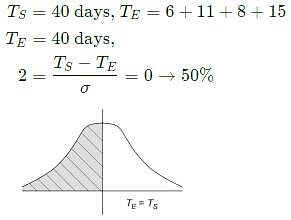
Activities A, B, C and D form the critical path for a project with a PERT network. The means and variances of the activity duration for each activity are given below. All activity durations follow the Gaussian (normal) distribution, and are independent of each other.
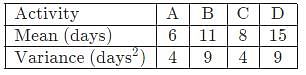
The probability that the project will be completed within 40 days is _____ (round off to two decimal places).
(Note: Probability is a number between 0 and 1).

The probability that the project will be completed within 40 days is _____ (round off to two decimal places).
(Note: Probability is a number between 0 and 1).
Consider the following network of activities, with each activity named A-L, illustrated in the nodes of the network

The number of hours required for each activity is shown alongside the nodes. The slack on the activity L, is ________ hours.
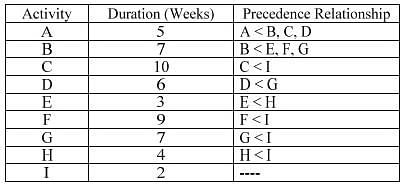
The activities of a project, their duration and the precedence relationships are given in the table. For example, in a precedence relationship "X < Y < Z" means that X is predecessor of activities Y and Z. The time to complete the activities along the critical path is ______ weeks.
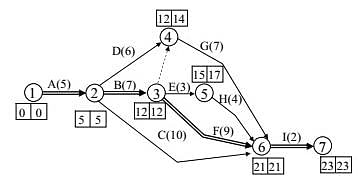
Following data refers to the activities of a project, where, node 1 refers to the start and node 5 refers to the end of the project.
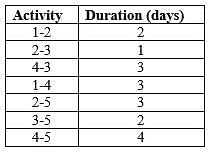
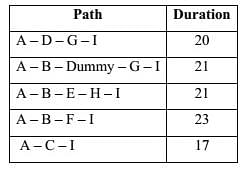
The critical path (CP) in the network is
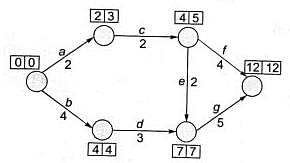
A project consists of 7 activities. The network along with the time durations (in days) for various activities is shown in the figure.
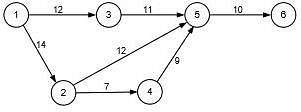
The minimum time (in days) for completion of the project is_________
A sample of 15 data is follows: 17, 18, 17, 17, 13, 18, 5, 5, 6, 7, 8, 9, 20, 17, 3. The mode of the data is
The precedence relations and duration (in days) of activities of a project network are given in the table. The total float (in days) of activities e and f, respectively, are

A project has six activities (A to F) with respective activity durations 7,5,6,6,8,4 days. The network has three paths A-B,C-D and E-F. All the activities can be crashed with the same crash cost per day. The number of activities that need to be crashed to reduce the project duration by 1 day is