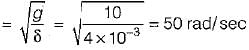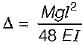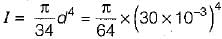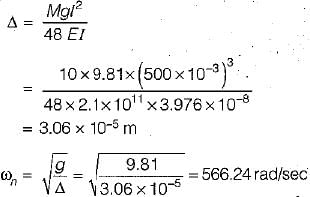Test: Linear Vibration Analysis - 2 - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Linear Vibration Analysis - 2
All of the following statements are correct, except,
The governing equation of a specific simple vibrating system is
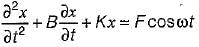
The system is subjected to
The static deflection of a shaft under a flywheel is 4 mm. Take g = 10 m/s2. What is the critical speed in rad/s?
A flexible rotor-shaft system comprises of a 10 kg rotor disc placed in the middle of a massless shaft of diameter 30 mm and length 500 mm between bearings (shaft is being taken massless as the equivalent mass of the shaft is included in the rotor mass) mounted at the ends. The shaft is made of steel for which the value of E is 2.1 x 1011 Pa. What is the critical speed of rotation of the shaft.
When a body is subjected ,to transverse vibration, the stress induced in the body will be
Whirling speed of a shaft coincides with the natural frequency of its
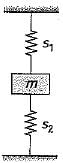
For given figure shows a spring mass system where the mass m is fixed in between two springs of stiffness s1 and s2. What is the equivalent spring stiffness
The rate of decay of oscillations is known as




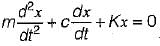 represents
represents