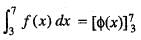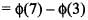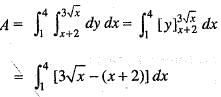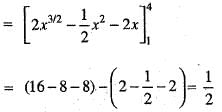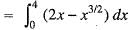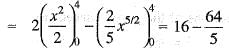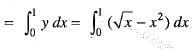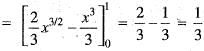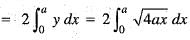Integral Calculus -8 - Mathematics MCQ
20 Questions MCQ Test - Integral Calculus -8
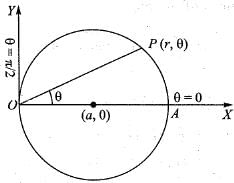
The volume of the solid generated by the revolution of r = 2a cos θ about the initial line is given by:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
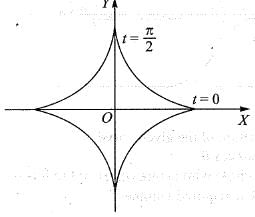
The surface area of the solid generated by the revolution of the curve x = a cos3t, y = a sin3 t about x-axis is given by:
Evaluate the integral of (3x2 + 9y2) dx dy if the interior limits has an upper limit of y and a lower limit of 0, and whose outer limit has an upper limit of 2 and a lower limit of 0.
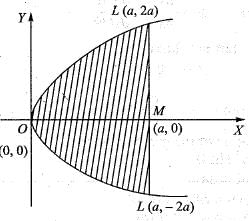
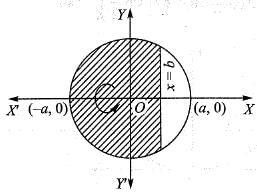
The segment o f the circle x2 + y2 = a2 cut off by the chord x = b (0 < b < a) revolves about the x-axis and generates the solid known as a segment of a sphere. The volume of this solid is:
The surface area of the solid generated by the revolution of the curve r2 = a2 cos 2θ about a tangent at the pole is given by:
The area bounded by the curve y = sin x, x-axis and the lines x = 0, x = π is revolved about y-axis. The surface of revolution is equal to:
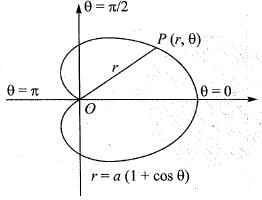
The surface of the solid formed by the revolution o f the cardioid r = a (1 + cos θ) about the initial line is given by:
The length of the are of the curve
x sin θ + y cos θ = f' (θ),
x cos θ - y cos θ = f " (θ)
is given by:
The volume of the solid generated by the revolution of the cardioid r = a(1 + cos θ) about the initial line is given by
The ratio of areas bounded by the curve a4y2 = x5(2a -x) and the circle of radius a is:
By taking (a, 0) as the fixed point, the intrinsic equation of the astroid x2/3 + y2/3 = a2/3 is given by:
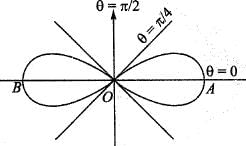
The volume of the solid generated by the revolution of the lemniscate r2 = a2 cos2θ about the line 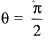 is given by:
is given by:
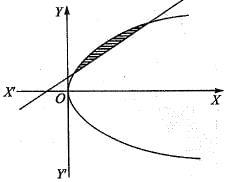
The area bounded by the curves y2 = 9x, x - y + 2 = 0 is given by:
The area bounded by the curve y2 = x3 and the line y = 2x is given by:
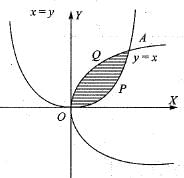
The area bounded by the curve x2 = y and y2 = x is given by:
The area bounded by the parabola y2 = 4ax and its latus rectum is given by


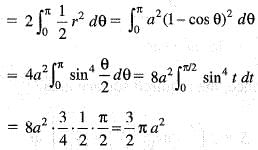
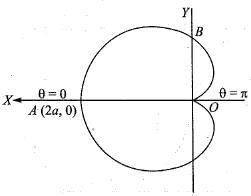
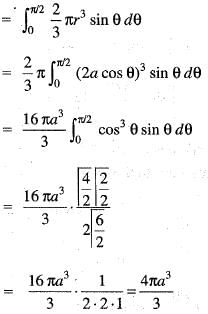
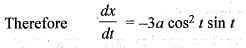
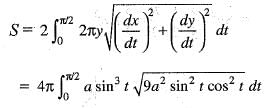
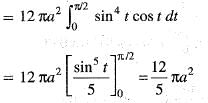
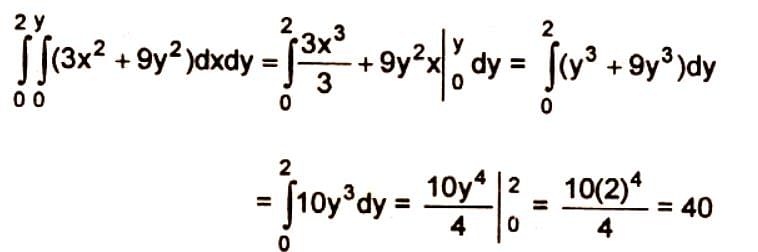
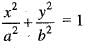 is given by:
is given by: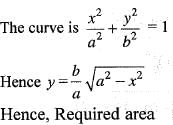
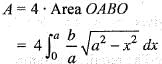
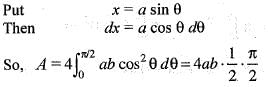
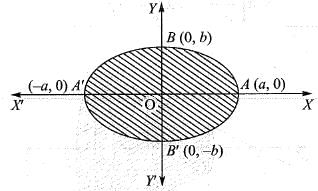
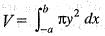
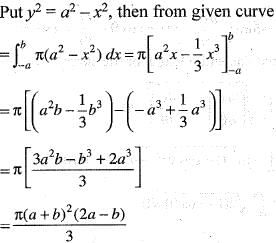
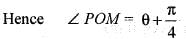
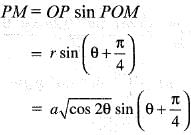
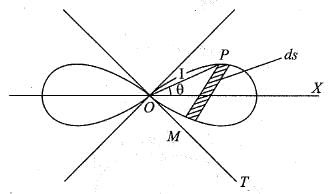

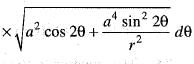
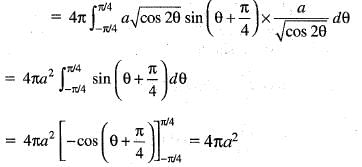
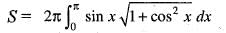
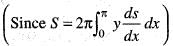
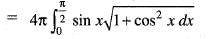
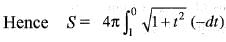
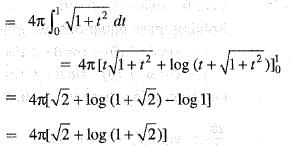
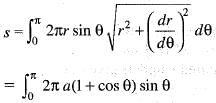
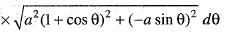
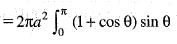
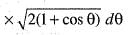
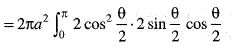
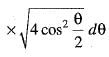
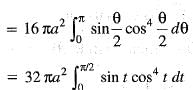
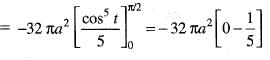
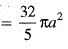

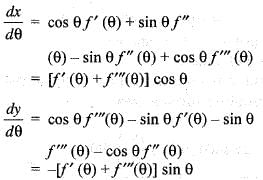
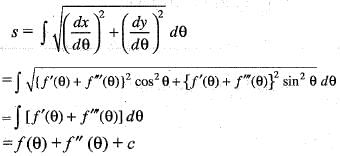
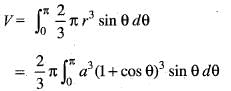
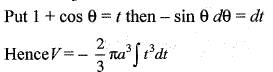
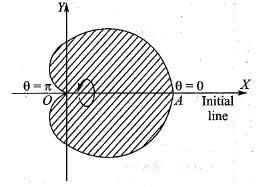
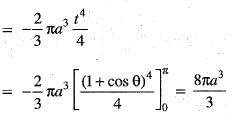

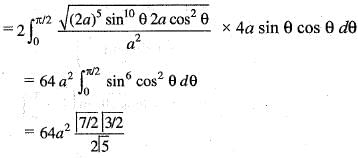
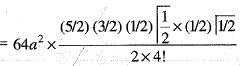

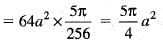
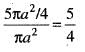
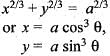

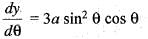
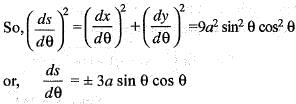
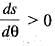
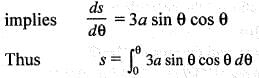
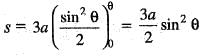 ..(i)
..(i)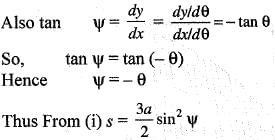
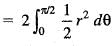
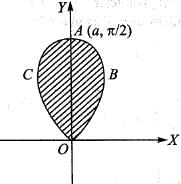
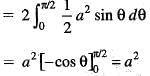
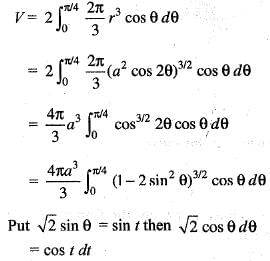
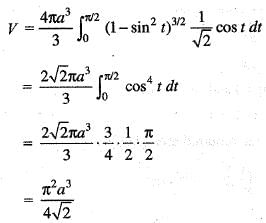
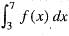 is equal to:
is equal to: