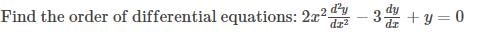Differential Equations - 3 - Mathematics MCQ
20 Questions MCQ Test - Differential Equations - 3
Solving by variation of parameter y" - 2y'+ y = exlog x, the value of wronskion W is
The c-discriminant of the equations
(y - c)2 = x(x - a)2 is
(y - c)2 = x(x - a)2 is
If y1(x) and y2(x) are solutions of y" + x2y' + (1 - x)y = 0 such that
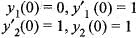
then the Wronskian W( y1, y2) on R is
If y1 and y2 are two solutions of initial value problem y" + p(x)y' + q(x)y = 0, y(x0) = y0, y'(x0) = y0 and the Wronskion W(y1, y2) = 0, then y1 and y2 are
Which of the following transformation reduce the differential equation  into the form
into the form 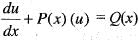
For IVP
y’ = 2y1/2, y(0) = 0
Which one is correct in a nbd of 0?
The degree of differential equation satisfying the relation 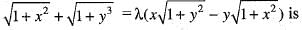
The process of formation of the differential equation is given in the wrong order, select the correct option from below given options.
1) Eliminate the arbitrary constants.
2) Differential equation which involves x, y, dy / dx
3) Differentiating the given equation w.r.t x as many times as the number of arbitrary constants.
The singular solution of the differential equation p3 + px - y = 0 is
Solving by variation of parameter for the equation y" + y = sec x, the value of Wronskion is
The eigen values for the boundary value problem x" + λx = 0; x(0) = 0, x(π) + x'(π) = 0 satisfy
Suppose yp(x) = x cos 2(x) is a particular solution of y" + αy = - 4 sin (2x)
Then, the constant α equals
All real solutions of the differential equation y" + 2ay' + by = cos x (where a and b are real constants) are periodic if
Integrating factor of (x7y2 + 3y)dx + (3x8y - x)dy = 0 is xmyn, then


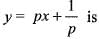
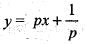
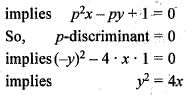

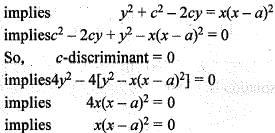
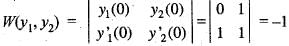
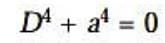 is
is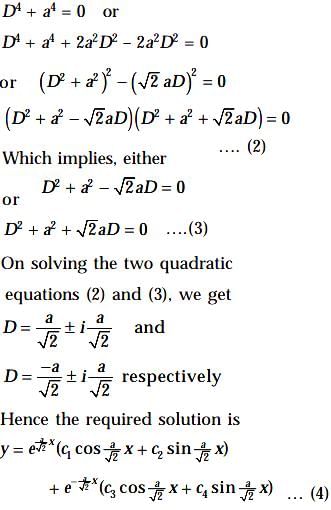
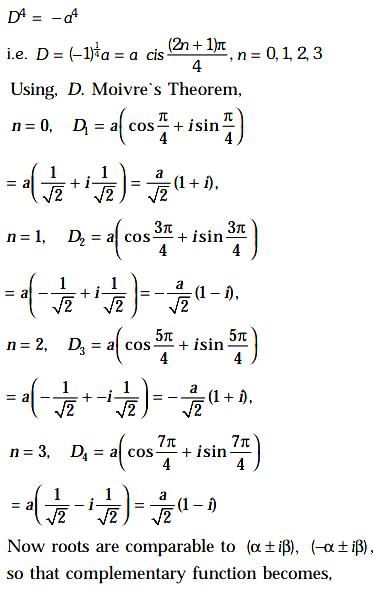
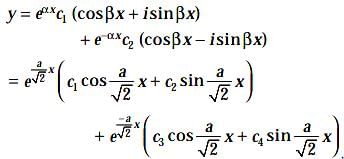
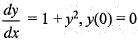 in the domain R : |x| < 5, |y| < 3 the equation has
in the domain R : |x| < 5, |y| < 3 the equation has