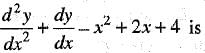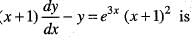Differential Equations - 8 - Mathematics MCQ
20 Questions MCQ Test - Differential Equations - 8
General solution of equation (sin x - x cos x)y" - (x sin x) y' + (sin x)y = 0, given that y = sin x is a solution
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The equation 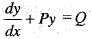 is linear differential equation of first order, if
is linear differential equation of first order, if
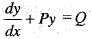 is linear differential equation of first order, if
is linear differential equation of first order, ifAn integrating factor of x dy/dx + (3x + 1)y = xe–2x is
What is the reason behind the non-existence of any real function which satisfies the differential equation, (y’)2 + 1 = 0?
What is the order of the partial differential equation,
A particular integral of y" - (a + b)y' + aby = Q(x) is,
The homogeneous differential equation M(x, y)dx, N(x, y) dy = 0 can be reduced to a differential equation, In which the variable are separated, by the substitution
In linear ordinary differential equation, the dependent variable and its differential coefficients are not multiplied together and occurs only in
General solution of the equation 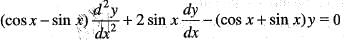 Given that y = sin x is a solution, is
Given that y = sin x is a solution, is
Solve d3y/dx3 - d2y/dx2 - 4dy/dx + 4y = 0 has the solution
The P.I. of the differential equation (D3 - D)y = ex + e-x, 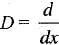 is
is
If φ(x, y) = 0 is a singular solution, then φ(x, y) is a factor of
A differential equation of first order and first degree is homogeneous, if
Given, an equation 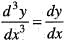 and a solution of it is y = a0 + a1 sinh x + a2 cosh x, where a0, a1, a2 are arbitrary constants, then this solution is
and a solution of it is y = a0 + a1 sinh x + a2 cosh x, where a0, a1, a2 are arbitrary constants, then this solution is


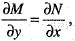 then
then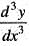
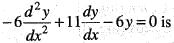
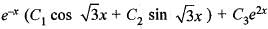 is the general solution of
is the general solution of