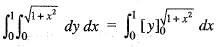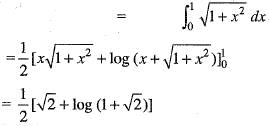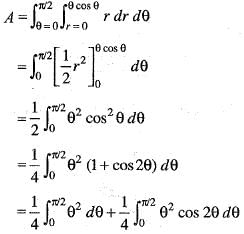Test: Double And Triple Integrals - 2 - Mathematics MCQ
20 Questions MCQ Test - Test: Double And Triple Integrals - 2
The volume of an object expressed in spherical coordinates is given by 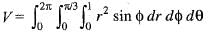
Q. The value of the integral is
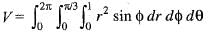
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
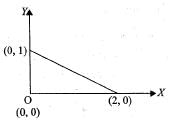
Consider the shaded triangular region P shown in the figure. What is  xy dxdy?
xy dxdy?
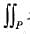 xy dxdy?
xy dxdy?
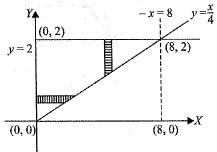
Changing the order of integration in the double integral 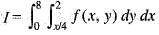 leads to
leads to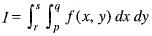 , then the value of q is
, then the value of q is
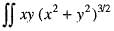 dxdy over the positive quadrant of the circle x2 + y2 = 1 is given by
dxdy over the positive quadrant of the circle x2 + y2 = 1 is given by
The volume of the cylinder x2 + y2 = a2 bounded below by z = 0 and bounded above by z = h is given by
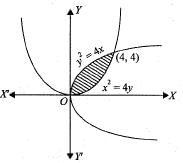
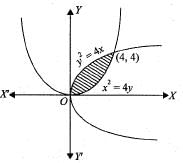
If A is the region bounded by the parabolas y2 = 4x and x2 = 4y, then 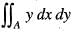 is equal to
is equal to
If A is the region bounded by the parabolas y2 = 4x and x2 = 4y, then 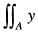 dxdy is equal to
dxdy is equal to
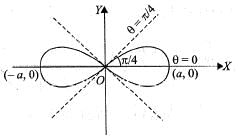
The area of the lemniscate r2 = a2 cos2θ is given by
The area bounded by the curves y2 = 9x, x —y + 2 = 0 is given by
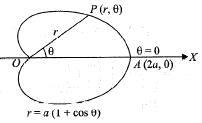
The area of the cardioid r = a (1 + cosθ) is given by
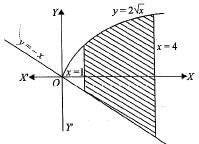
The area bounded by the curves y = 2√x, y = - x, x = 1 and x = 4 is given by
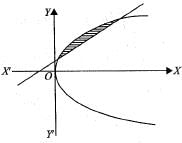
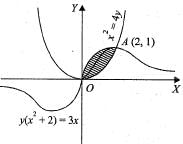
The area o f the region bounded by the curve y(x2 + 2 ) = 3x and 4y = x2 is given by
The area bounded by the curve r = θ cosθ and the lines θ = 0 and θ = π/2 is given by
The solution of the differential equation dy/dx = x log x is


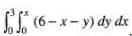 dxdy is
dxdy is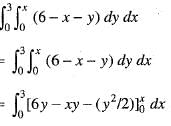
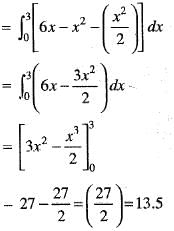
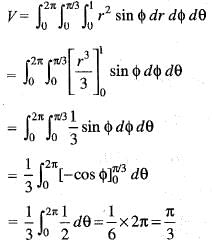
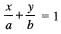
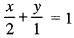

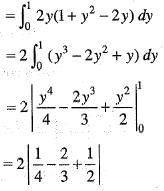
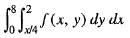
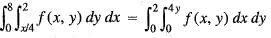
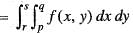
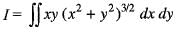
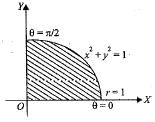
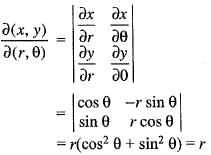
 = 1/14
= 1/14
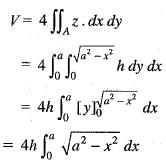
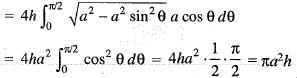
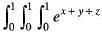 dxdydz is equal to
dxdydz is equal to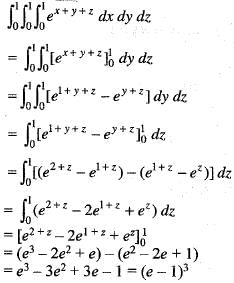
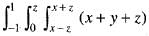 dydxdz is equal to
dydxdz is equal to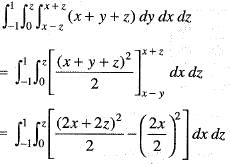
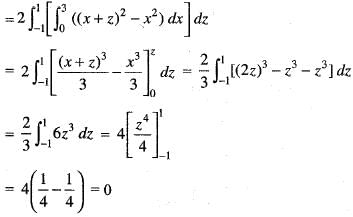
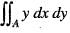
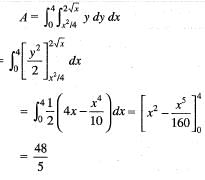



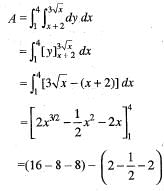
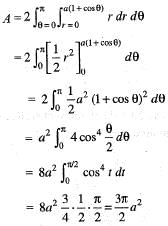
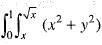 dydx is equal to
dydx is equal to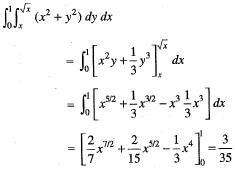
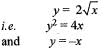
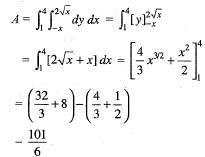
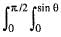 rdθdr is given by
rdθdr is given by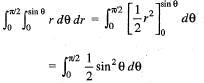
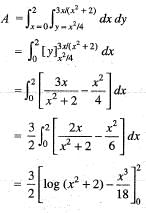
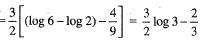
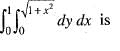
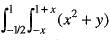 dydx
dydx