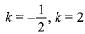Class 10 Exam > Class 10 Tests > RS Aggarwal Test: Coordinate Geometry - Class 10 MCQ
RS Aggarwal Test: Coordinate Geometry - Class 10 MCQ
Test Description
10 Questions MCQ Test - RS Aggarwal Test: Coordinate Geometry
RS Aggarwal Test: Coordinate Geometry for Class 10 2024 is part of Class 10 preparation. The RS Aggarwal Test: Coordinate Geometry questions and answers have been prepared
according to the Class 10 exam syllabus.The RS Aggarwal Test: Coordinate Geometry MCQs are made for Class 10 2024 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for RS Aggarwal Test: Coordinate Geometry below.
Solutions of RS Aggarwal Test: Coordinate Geometry questions in English are available as part of our course for Class 10 & RS Aggarwal Test: Coordinate Geometry solutions in
Hindi for Class 10 course.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free. Attempt RS Aggarwal Test: Coordinate Geometry | 10 questions in 10 minutes | Mock test for Class 10 preparation | Free important questions MCQ to study for Class 10 Exam | Download free PDF with solutions
RS Aggarwal Test: Coordinate Geometry - Question 1
The mid-point of the line segment joining the points A (-2, 8) and B (-6, -4) is
Detailed Solution for RS Aggarwal Test: Coordinate Geometry - Question 1
RS Aggarwal Test: Coordinate Geometry - Question 2
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is
Detailed Solution for RS Aggarwal Test: Coordinate Geometry - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
RS Aggarwal Test: Coordinate Geometry - Question 3
The distance of the point P (2, 3) from the x-axis is
Detailed Solution for RS Aggarwal Test: Coordinate Geometry - Question 3
RS Aggarwal Test: Coordinate Geometry - Question 4
If 
is the mid-point of the line segment joining the points Q (-6, 5) and E (-2, 3), then the value of a is
Detailed Solution for RS Aggarwal Test: Coordinate Geometry - Question 4
RS Aggarwal Test: Coordinate Geometry - Question 5
The distance of the point P (-6, 8) from the origin is
RS Aggarwal Test: Coordinate Geometry - Question 6
The points (k + 1, 1), (2k + 1, 3) and (2k + 2, 2k) are collinear if
Detailed Solution for RS Aggarwal Test: Coordinate Geometry - Question 6
RS Aggarwal Test: Coordinate Geometry - Question 8
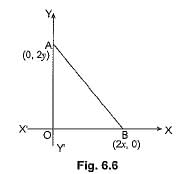
The coordinates of the point which is equidistant from the three vertices of the triangle shown in the given Fig. 6.6 are
RS Aggarwal Test: Coordinate Geometry - Question 9
The area of a triangle with vertices A (3, 0), B (7, 0) and C (8, 4) is
RS Aggarwal Test: Coordinate Geometry - Question 10
The points which lies on the perpendicular bisector of the line segment joining the points A (-2, -5), B (2, 5) is
Detailed Solution for RS Aggarwal Test: Coordinate Geometry - Question 10
Information about RS Aggarwal Test: Coordinate Geometry Page
In this test you can find the Exam questions for RS Aggarwal Test: Coordinate Geometry solved & explained in the simplest way possible.
Besides giving Questions and answers for RS Aggarwal Test: Coordinate Geometry, EduRev gives you an ample number of Online tests for practice
Download as PDF
Top Courses for Class 10
Important Questions for RS Aggarwal Test: Coordinate Geometry
Find all the important questions for RS Aggarwal Test: Coordinate Geometry at EduRev.Get fully prepared for RS Aggarwal Test: Coordinate Geometry with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the RS Aggarwal Test: Coordinate Geometry syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of RS Aggarwal Test: Coordinate Geometry resources.
RS Aggarwal Test: Coordinate Geometry MCQs with Answers
Prepare for the RS Aggarwal Test: Coordinate Geometry within the Class 10 exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for RS Aggarwal Test: Coordinate Geometry
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace RS Aggarwal Test: Coordinate Geometry with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup