Test: Determinacy & Indeterminacy - 3 - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Determinacy & Indeterminacy - 3
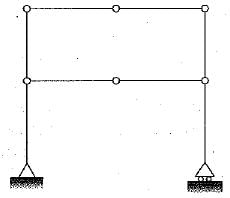
Neglecting axial deformation, the kinematic indeterminacy of the structure shown in the figure below is:
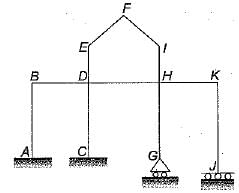

What is the statical indeterminacy for the frame shown below?
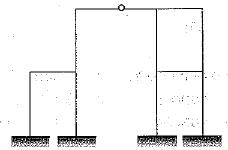

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The statical indeterminacy for the given 3D frame is

The statical indeterminacy for the given 2D frame is
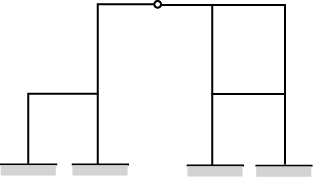
Consider the following pin-jointed plane frames
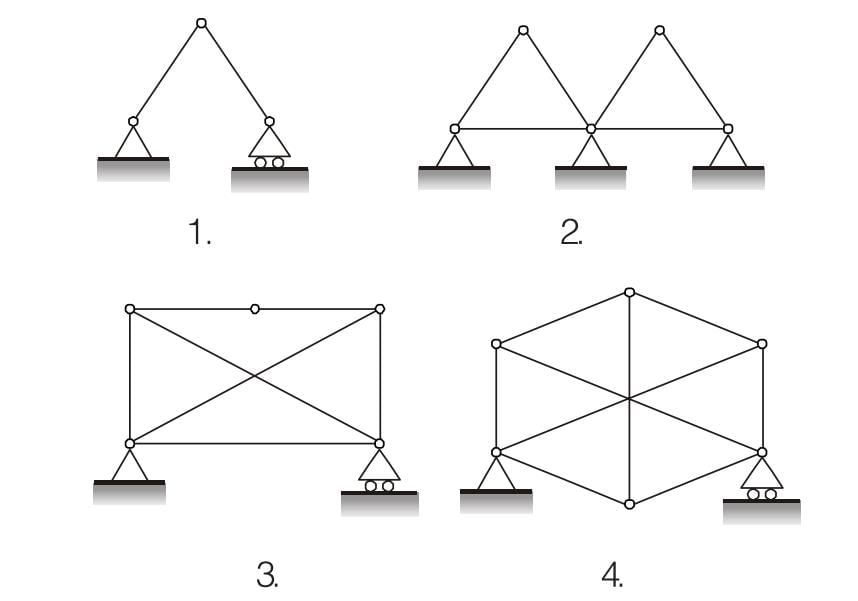
Which of these frames are stable?
The kinematics indeterminacy of the beam as shown in figure is

The degree of static indeterminacy of the hybrid plane frame as shown in figure is
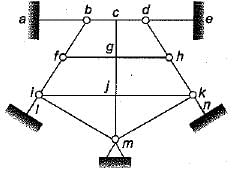
A plane frame ABCDEFGH shown in figure has clamp support at A hinge supports at G and H, axial force release at C and moment release (hinge) at E. The static (ds) and kinematic (αk) indeterminacies respectively are
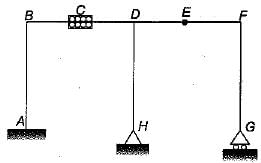
The total degree of kinematic indeterminacy of the plane frame shown in the given figure considering columns to be axially rigid is
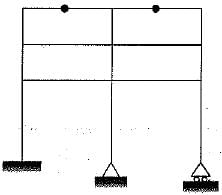
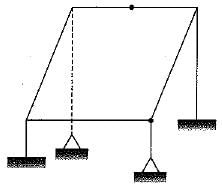
The plane pin joint structure shown in figure below is


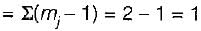
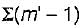
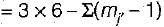
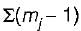 = (2 - 1) + (2 - 1) = 2
= (2 - 1) + (2 - 1) = 2














