Test: Torsion of Shafts - 3 - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Torsion of Shafts - 3
For a circular shaft of diameter d subjected to torque T, the maximum value of the shear stress is
A stepped steel shaft shown below is subjected to 10 N-m torque. If the modulus of rigidity is 80 GPa, the strain energy in the shaft in N-mm is


| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
While transmitting the same power by a shaft, if its speed is doubled, what should be its new diameter if the maximum shear stress induced in the shaft remains same?
A solid shaft of diameter 100 mm, length 1000 mm is subjected to a twisting moment ‘T’, the maximum shear stress developed in the shaft is 60 N/mm2. A hole of 50 mm diameter is now drilled throughout the length of the shaft. To developed a maximum shear stress of 60 N/ mm2 in the hollow shaft, the torque ‘ T must be reduced by
Maximum shear stress developed on the surface - of a solid circular shaft under pure torsion is 240 MPa. If the shaft diameter is doubled then the maximum shear stress developed corresponding to the same torque will be
A circular shaft is subjected to a twisting moment T and bending moment M. The ratio of maximum bending stress to maximum shear stress is given by
A section of a solid circular shaft with diameter D is subjected to bending moment M and torque T. The expression for maximum principal stress at the section is
Two shafts, one of solid section and the other of hollow section, of same material and weight having same length are subjected to equal torsional force. What is the torsional stiffness of hollow shaft?
A long shaft of diameter d is subjected to twisting moment T at its ends. The maximum normal stress acting at its cross-section is equal to
A circular shaft shown in the figure is subjected to torsion T at two points A and B. The torsional rigidity of portions CA and BD is GJ1 and that of portion AB is GJ2. The rotations of shaft at points A and B are q1 and q2. The rotation q1 is



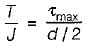
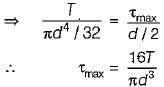

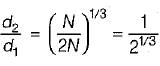
 ............... (i)
............... (i) .................. (ii)
.................. (ii)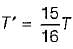


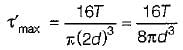

 = 30 MPa
= 30 MPa

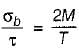
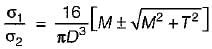




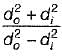 is always greater than 1
is always greater than 1
















