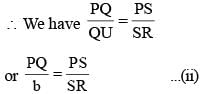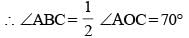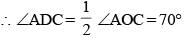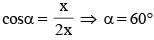Test: Geometry - CAT MCQ
30 Questions MCQ Test - Test: Geometry
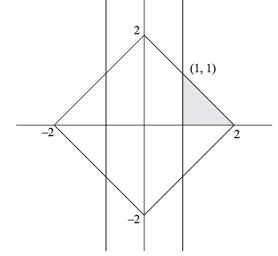
Let S be the set of all points (x, y) in the x-y plane such that |x| + |y| ≤ 2 and |x| ≥ 1. Then, the area (in square units) of the region represented by S equals
(2019)
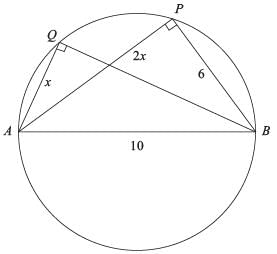
AB is a diameter of a circle of radius 5 cm. Let P and Q be two points on the circle so that the length of PB is 6 cm, and the length of AP is twice that of AQ. Then the length, in cm, of QB is nearest to
(2019)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
With rectangular axes of coordinates, the number of paths from (1, 1) to (8, 10) via (4, 6), where each step from any point (x, y) is either to (x, y + 1) or to (x + 1, y), is
(2019)
Let T be the triangle formed by the straight line 3x + 5y – 45 = 0 and the coordinate axes. Let the circumcircle of T have radius of length L, measured in the same unit as the coordinate axes. Then, the integer closest to L is
(2019)
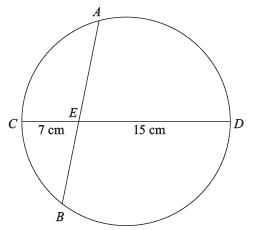
In a circle of radius 11 cm, CD is a diameter and AB is a chord of length 20.5 cm. If AB and CD intersect at a point E inside the circle and CE has length 7 cm, then the difference of the lengths of BE and AE, in cm, is
(2019)
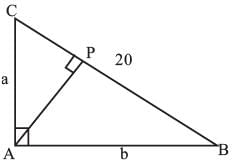
Let ABC be a right-angled triangle with hypotenuse BC of length 20 cm. If AP is perpendicular on BC, then the maximum possible length of AP, in cm, is
(2019)
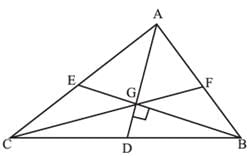
In a triangle ABC, medians AD and BE are perpendicular to each other, and have lengths 12 cm and 9 cm, respectively. Then, the area of triangle ABC, in sq cm, is
(2019)
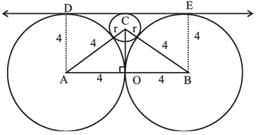
Two circles, each of radius 4 cm, touch externally. Each of these two circles is touched externally by a third circle. If these three circles have a common tangent then the radius of the third circle, in cm, is
(2019)
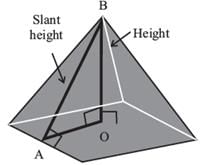
The base of a regular pyramid is a square and each of the other four sides is an equilateral triangle, length of each side being 20 cm. The vertical height of the pyramid, in cm, is
(2019)
A man makes complete use of 405 cc of iron, 783 cc of aluminium, and 351 cc of copper to make a number of solid right circular cylinders of each type of metal. These cylinders have the same volume and each of these has radius 3 cm. If the total number of cylinders is to be kept at a minimum, then the total surface area of all these cylinders, in sq cm, is
(2019)
Let A and B be two regular polygons having a and b sides, respectively. If b = 2a and each interior angle of B is 3/2 times each interior angle of A, then each interior angle, in degrees, of a regular polygon with a + b sides is
(2019)
Points E, F, G, H lie on the sides AB, BC, CD, and DA, respectively, of a square ABCD. If EFGH is also a square whose area is 62.5% of that of ABCD and CG is longer than EB, then the ratio of length of EB to that of CG is
(2018)
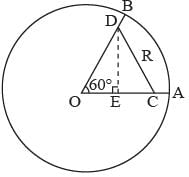
In a circle with center O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is
(2018)
In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is
(2018)
In a circle, two parallel chords on the same side of a diameter have lengths 4 cm and 6 cm. If the distance between these chords is 1 cm, then the radius of the circle, in cm, is
(2018)
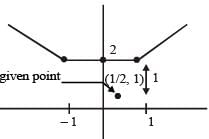
The shortest distance of the point  from the curve y = |x – 1| + |x + 1| is
from the curve y = |x – 1| + |x + 1| is
(2017)
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq cm, of the region enclosed by BPC and BQC is
(2017)
From a triangle ABC with sides of lengths 40 ft, 25 ft and 35 ft, a triangular portion GBC is cut off where G is the centroid of ABC. The area, in sq ft, of the remaining portion of triangle ABC is
(2017)
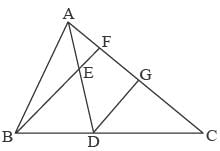
In the figure below, BD = 8 cm and DC = 6 cm. AE : ED = 3 : 4. If AF =12 cm, find AC (in cm).
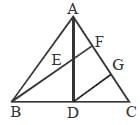
(2016)
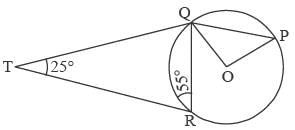
In the figure below, P, Q and R are points on a circle with centre O. The tangent to the circle at R intersects secant PQ at T. If ∠QRT = 55° and ∠QTR = 25°, find ∠POQ.
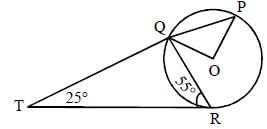
(2016)
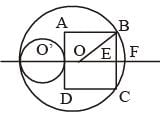
In the figure, O and O’ are the centres of the bigger and smaller circles respectively and small circle touches the square ABCD at the mid point of side AD. The radius of the bigger circle is equal to 15 cm and the side of the square ABCD is 18 cm. Find the radius of the smaller circle.

(2015)
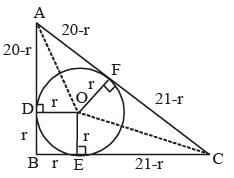
ΔABC is a right angled triangle, with ∠B = 90o, AB = 20 cm and BC = 21cm. A circle with centre O is inscribed in triangle ABC. OD, OE and OF are perpendiculars drawn on the sides AB, BC and CA respectively. Find the ratio of the area of the quadrilateral FOEC to the area of the quadrilateral ADOF.
(2015)
An isosceles right angled triangle with length of its equal sides being 30 cm, is rotated 180° about its centroid to form a new triangle. Find the area of the region common to the original and the new triangles.
(2015)
The line √3y = x is the radius of the circle, it meets the circle centred at origin O at point M(√3,1) If PQ is the tangent to the circle at M as shown, find the length of the PQ.
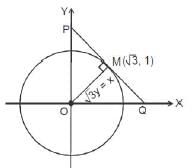
(2015)
In the given figure, AB is the diameter of the circle with centre O. If ∠BOD = 15º, ∠EOA = 85º, then find the measure of ∠ECA.
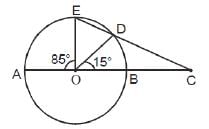
(2015)
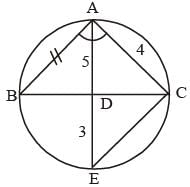
The bisector of ÐBAC of Δ ABC cuts BC at D and the circumcircle of the triangle at E. If DE = 3 cm, AC = 4 cm and AD = 5 cm, then the length of AB is
(2014)
Let S be an arbitrary point on the side PQ of an acute-angled D PQR. Let T be the point of intersection of QR and the straight line PT drawn parallel to SR through P. Let U be the point of intersection of PR and the straight line QU drawn parallel to SR through Q. If PT = a units and QU = b units, then the length of SR is
(2014)
ABCD is a rectangle with points E and F lying on sides AB and CD respectively. If the area of quadrilateral AEFD equals the area of quadrilateral CBEF, then which of the following statements is necessarily false with respect to the rectangle ABCD?
(2014)
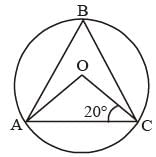
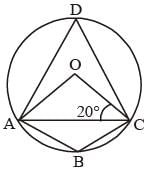
AC is a chord of a circle whose centre is at O. If B is any point on the arc AC and ∠OCA = 20°, then the magnitude of ∠ABC is
(2014)
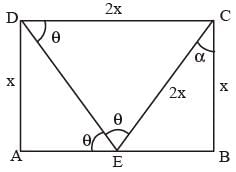
E is a point on the side AB of a rectangle ABCD, the adjacent sides of which are in the ratio 2 : 1. If ∠AED = ∠DEC, then what is the measure of ∠AED?
(2013)


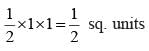
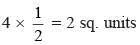
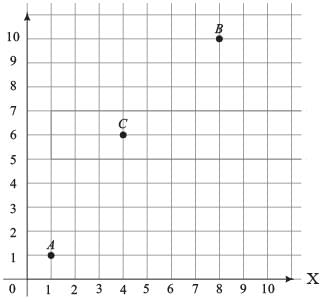
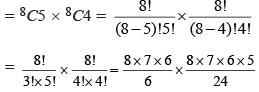
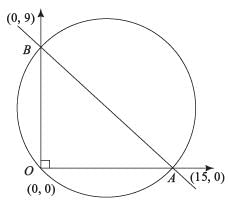
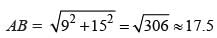
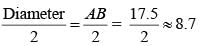
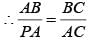 [Ratio of corresponding sides of two similar triangles are equal]
[Ratio of corresponding sides of two similar triangles are equal]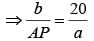
 ...(ii)
...(ii)
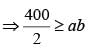
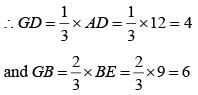
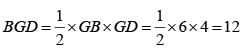
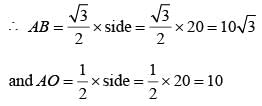
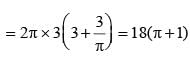
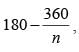 where ‘n’
where ‘n’ 
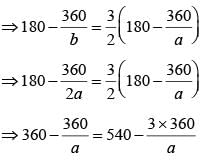
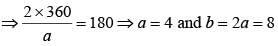

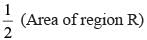
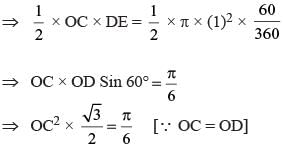
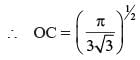
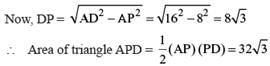
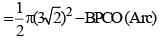 ...(i)
...(i)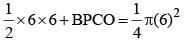
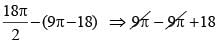 = 18 sq cm
= 18 sq cm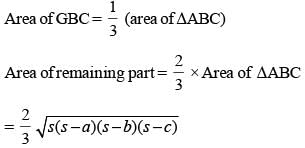
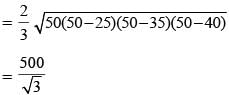
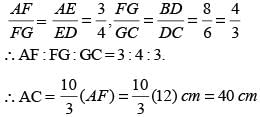

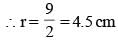
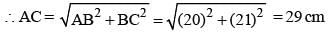


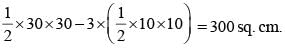
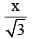
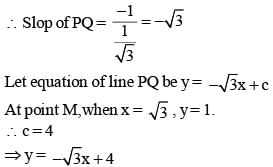
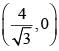 and Co-ordinates of point P = (0, 4).
and Co-ordinates of point P = (0, 4).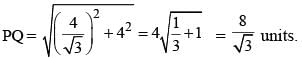
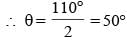



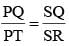
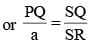 ...(i)
...(i)