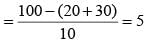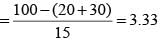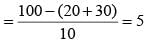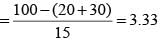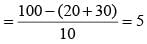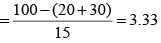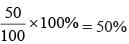Test: Analytical Reasoning - CAT MCQ
30 Questions MCQ Test - Test: Analytical Reasoning
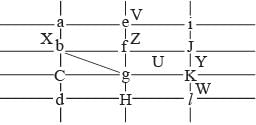
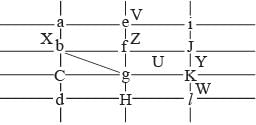
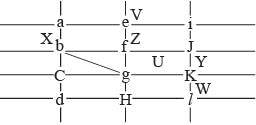
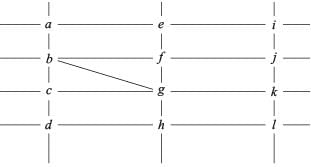
Directions for Questions: The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at intersection f.

Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
(2019)
Q. Who is standing at intersection a?

Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
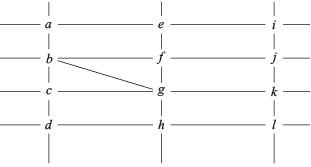
Directions for Questions: The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at intersection f.
Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
(2019)
Q. Who can V see?

Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
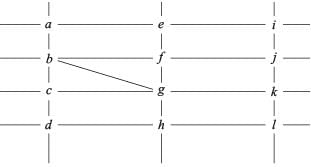
Directions for Questions: The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at intersection f.
Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
(2019)
Q. What is the minimum number of street segments that X must cross to reach Y?

Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
Directions for Questions: The figure below shows the street map for a certain region with the street intersections marked from a through l. A person standing at an intersection can see along straight lines to other intersections that are in her line of sight and all other people standing at these intersections. For example, a person standing at intersection g can see all people standing at intersections b, c, e, f, h, and k. In particular, the person standing at intersection g can see the person standing at intersection e irrespective of whether there is a person standing at intersection f.
Six people U, V, W, X, Y, and Z, are standing at different intersections. No two people are standing at the same intersection.
The following additional facts are known.
1. X, U, and Z are standing at the three corners of a triangle formed by three street segments.
2. X can see only U and Z.
3. Y can see only U and W.
4. U sees V standing in the next intersection behind Z.
5. W cannot see V or Z.
6. No one among the six is standing at intersection d.
(2019)
Q. Should a new person stand at intersection d, who among the six would she see?
Directions for Questions: A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
(2019)
Q. In how many different ways can the items be arranged on the shelves?
Directions for Questions: A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
(2019)
Q. Which of the following items is not a type of biscuit?
Directions for Questions: A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
(2019)
Q. Which of the following can represent the numbers of the empty shelves in a possible arrangement?
Directions for Questions: A supermarket has to place 12 items (coded A to L) in shelves numbered 1 to 16. Five of these items are types of biscuits, three are types of candies and the rest are types of savouries. Only one item can be kept in a shelf. Items are to be placed such that all items of same type are clustered together with no empty shelf between items of the same type and at least one empty shelf between two different types of items. At most two empty shelves can have consecutive numbers.
The following additional facts are known.
1. A and B are to be placed in consecutively numbered shelves in increasing order.
2. I and J are to be placed in consecutively numbered shelves both higher numbered than the shelves in which A and B are kept.
3. D, E and F are savouries and are to be placed in consecutively numbered shelves in increasing order after all the biscuits and candies.
4. K is to be placed in shelf number 16.
5. L and J are items of the same type, while H is an item of a different type.
6. C is a candy and is to be placed in a shelf preceded by two empty shelves.
7. L is to be placed in a shelf preceded by exactly one empty shelf.
(2019)
Q. Which of the following statements is necessarily true?
Directions for Questions: A new game show on TV has 100 boxes numbered 1, 2, . . . , 100 in a row, each containing a mystery prize. The prizes are items of different types, a, b, c, . . . , in decreasing order of value. The most expensive item is of type a, a diamond ring, and there is exactly one of these. You are told that the number of items at least doubles as you move to the next type. For example, there would be at least twice as many items of type b as of type a, at least twice as many items of type c as of type b and so on. There is no particular order in which the prizes are placed in the boxes.
(2019)
Q. Which of the following is not possible?
Directions for Questions: A new game show on TV has 100 boxes numbered 1, 2, . . . , 100 in a row, each containing a mystery prize. The prizes are items of different types, a, b, c, . . . , in decreasing order of value. The most expensive item is of type a, a diamond ring, and there is exactly one of these. You are told that the number of items at least doubles as you move to the next type. For example, there would be at least twice as many items of type b as of type a, at least twice as many items of type c as of type b and so on. There is no particular order in which the prizes are placed in the boxes.
(2019)
Q. You ask for the type of item in box 45. Instead of being given a direct answer, you are told that there are 31 items of the same type as box 45 in boxes 1 to 44 and 43 items of the same type as box 45 in boxes 46 to 100.
What is the maximum possible number of different types of items?
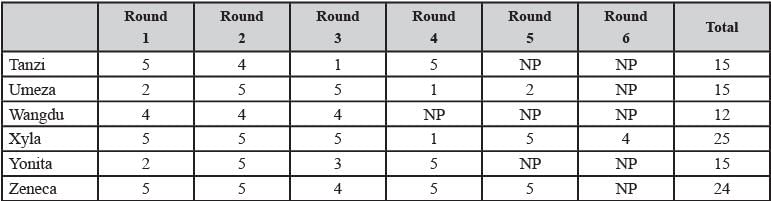
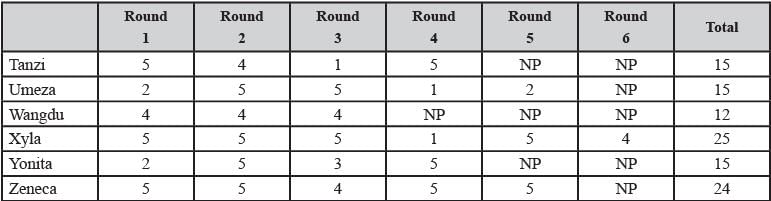
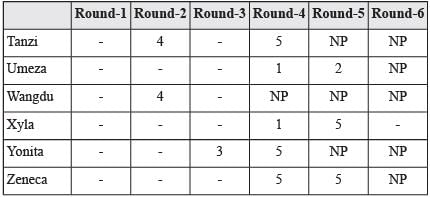
Directions for Questions: Six players – Tanzi, Umeza, Wangdu, Xyla, Yonita and Zeneca competed in an archery tournament. The tournament had three compulsory rounds, Rounds 1 to 3. In each round every player shot an arrow at a target. Hitting the centre of the target (called bull’s eye) fetched the highest score of 5. The only other possible scores that a player could achieve were 4, 3, 2 and 1. Every bull’s eye score in the first three rounds gave a player one additional chance to shoot in the bonus rounds, Rounds 4 to 6. The possible scores in Rounds 4 to 6 were identical to the first three.
A player’s total score in the tournament was the sum of his/ her scores in all rounds played by him/her. The table below presents partial information on points scored by the players after completion of the tournament. In the table, NP means that the player did not participate in that round, while a hyphen means that the player participated in that round and the score information is missing.

The following facts are also known.
1. Tanzi, Umeza and Yonita had the same total score.
2. Total scores for all players, except one, were in multiples of three.
3. The highest total score was one more than double of the lowest total score.
4. The number of players hitting bull’s eye in Round 2 was double of that in Round 3.
5. Tanzi and Zeneca had the same score in Round 1 but different scores in Round 3.
(2019)
Q. What was the highest total score?
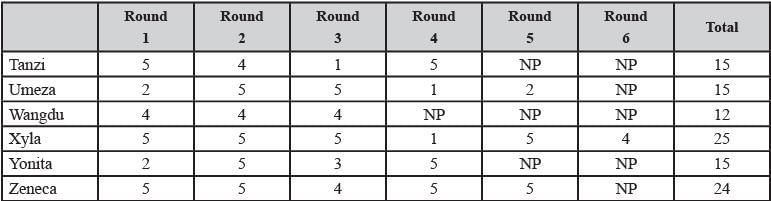
Directions for Questions: Six players – Tanzi, Umeza, Wangdu, Xyla, Yonita and Zeneca competed in an archery tournament. The tournament had three compulsory rounds, Rounds 1 to 3. In each round every player shot an arrow at a target. Hitting the centre of the target (called bull’s eye) fetched the highest score of 5. The only other possible scores that a player could achieve were 4, 3, 2 and 1. Every bull’s eye score in the first three rounds gave a player one additional chance to shoot in the bonus rounds, Rounds 4 to 6. The possible scores in Rounds 4 to 6 were identical to the first three.
A player’s total score in the tournament was the sum of his/ her scores in all rounds played by him/her. The table below presents partial information on points scored by the players after completion of the tournament. In the table, NP means that the player did not participate in that round, while a hyphen means that the player participated in that round and the score information is missing.
The following facts are also known.
1. Tanzi, Umeza and Yonita had the same total score.
2. Total scores for all players, except one, were in multiples of three.
3. The highest total score was one more than double of the lowest total score.
4. The number of players hitting bull’s eye in Round 2 was double of that in Round 3.
5. Tanzi and Zeneca had the same score in Round 1 but different scores in Round 3.
(2019)
Q. What was Zeneca’s total score?
Directions for Questions: Six players – Tanzi, Umeza, Wangdu, Xyla, Yonita and Zeneca competed in an archery tournament. The tournament had three compulsory rounds, Rounds 1 to 3. In each round every player shot an arrow at a target. Hitting the centre of the target (called bull’s eye) fetched the highest score of 5. The only other possible scores that a player could achieve were 4, 3, 2 and 1. Every bull’s eye score in the first three rounds gave a player one additional chance to shoot in the bonus rounds, Rounds 4 to 6. The possible scores in Rounds 4 to 6 were identical to the first three.
A player’s total score in the tournament was the sum of his/ her scores in all rounds played by him/her. The table below presents partial information on points scored by the players after completion of the tournament. In the table, NP means that the player did not participate in that round, while a hyphen means that the player participated in that round and the score information is missing.
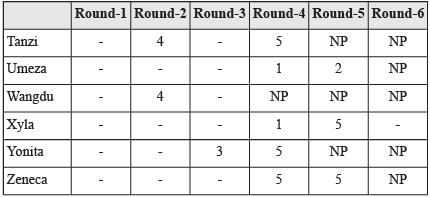
The following facts are also known.
1. Tanzi, Umeza and Yonita had the same total score.
2. Total scores for all players, except one, were in multiples of three.
3. The highest total score was one more than double of the lowest total score.
4. The number of players hitting bull’s eye in Round 2 was double of that in Round 3.
5. Tanzi and Zeneca had the same score in Round 1 but different scores in Round 3.
(2019)
Q. Which of the following statements is true?
Directions for Questions: Six players – Tanzi, Umeza, Wangdu, Xyla, Yonita and Zeneca competed in an archery tournament. The tournament had three compulsory rounds, Rounds 1 to 3. In each round every player shot an arrow at a target. Hitting the centre of the target (called bull’s eye) fetched the highest score of 5. The only other possible scores that a player could achieve were 4, 3, 2 and 1. Every bull’s eye score in the first three rounds gave a player one additional chance to shoot in the bonus rounds, Rounds 4 to 6. The possible scores in Rounds 4 to 6 were identical to the first three.
A player’s total score in the tournament was the sum of his/ her scores in all rounds played by him/her. The table below presents partial information on points scored by the players after completion of the tournament. In the table, NP means that the player did not participate in that round, while a hyphen means that the player participated in that round and the score information is missing.
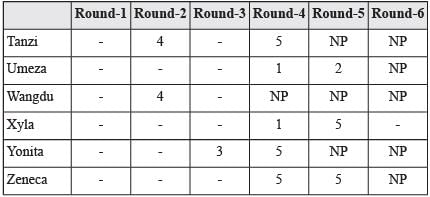
The following facts are also known.
1. Tanzi, Umeza and Yonita had the same total score.
2. Total scores for all players, except one, were in multiples of three.
3. The highest total score was one more than double of the lowest total score.
4. The number of players hitting bull’s eye in Round 2 was double of that in Round 3.
5. Tanzi and Zeneca had the same score in Round 1 but different scores in Round 3.
(2019)
Q. What was Tanzi’s score in Round 3?
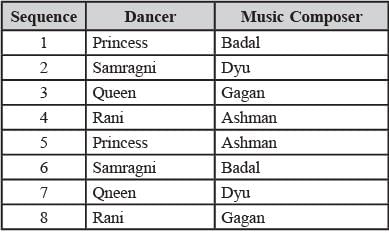
Directions for Questions: Princess, Queen, Rani and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
(i) No composer who assigned item to Princess, assigned any item to Queen.
(ii) No composer who assigned item to Rani, assigned any item to Samragni.
(iii) The first performance was by Princess; this item was assigned by Badal.
(iv) The last performance was by Rani; this item was assigned by Gagan.
(v) The items assigned by Ashman were performed consecutively.
The number of performances between items assigned by each of the remaining composers was the same.
(2019)
Q. Which of the following is true?
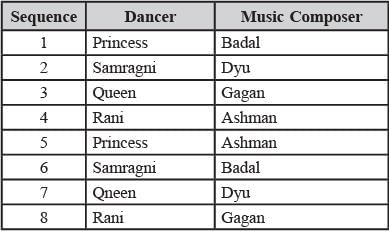
Directions for Questions: Princess, Queen, Rani and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
(i) No composer who assigned item to Princess, assigned any item to Queen.
(ii) No composer who assigned item to Rani, assigned any item to Samragni.
(iii) The first performance was by Princess; this item was assigned by Badal.
(iv) The last performance was by Rani; this item was assigned by Gagan.
(v) The items assigned by Ashman were performed consecutively.
The number of performances between items assigned by each of the remaining composers was the same.
(2019)
Q. Which of the following is FALSE?
Directions for Questions: Princess, Queen, Rani and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
(i) No composer who assigned item to Princess, assigned any item to Queen.
(ii) No composer who assigned item to Rani, assigned any item to Samragni.
(iii) The first performance was by Princess; this item was assigned by Badal.
(iv) The last performance was by Rani; this item was assigned by Gagan.
(v) The items assigned by Ashman were performed consecutively.
The number of performances between items assigned by each of the remaining composers was the same.
(2019)
Q. The sixth performance was composed by:
Directions for Questions: Princess, Queen, Rani and Samragni were the four finalists in a dance competition. Ashman, Badal, Gagan and Dyu were the four music composers who individually assigned items to the dancers. Each dancer had to individually perform in two dance items assigned by the different composers. The first items performed by the four dancers were all assigned by different music composers. No dancer performed her second item before the performance of the first item by any other dancers. The dancers performed their second items in the same sequence of their performance of their first items.
The following additional facts are known.
(i) No composer who assigned item to Princess, assigned any item to Queen.
(ii) No composer who assigned item to Rani, assigned any item to Samragni.
(iii) The first performance was by Princess; this item was assigned by Badal.
(iv) The last performance was by Rani; this item was assigned by Gagan.
(v) The items assigned by Ashman were performed consecutively.
The number of performances between items assigned by each of the remaining composers was the same.
(2019)
Q. Which pair of performances were composed by the same composer?
Directions for Questions: The first-year students in a business school are split into six sections. In 2019 the Business Statistics course was taught in these six sections by Annie, Beti, Chetan, Dave, Esha, and Fakir. All six sections had a common midterm (MT) and a common end term (ET) worth 100 marks each. ET contained more questions than MT. Questions for MT and ET were prepared collectively by the six faculty members. Considering MT and ET together, each faculty member prepared the same number of questions.
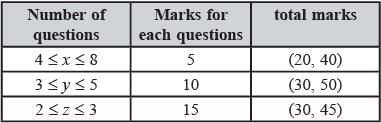
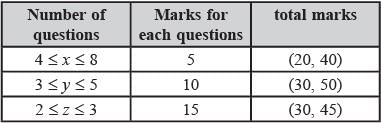
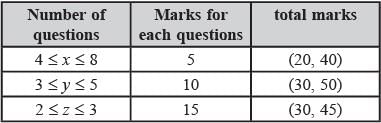
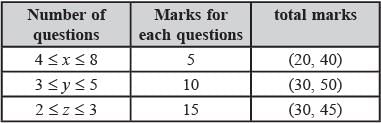
Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks. In both MT and ET, all the 5-mark questions preceded the 10-mark questions, and all the 15- mark questions followed the 10-mark questions.
The following additional facts are known.
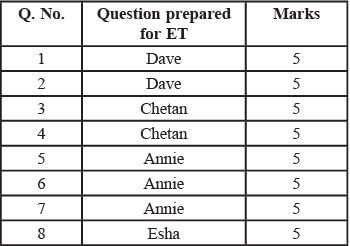
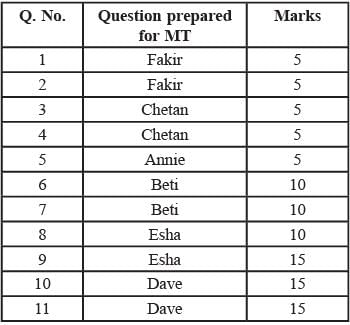
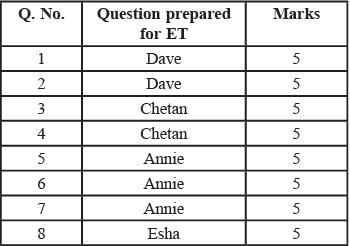
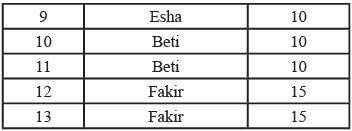
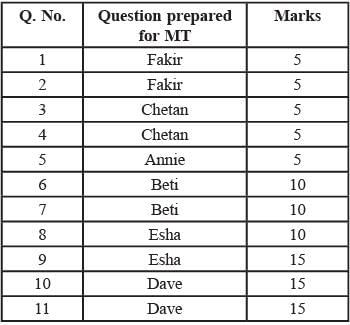
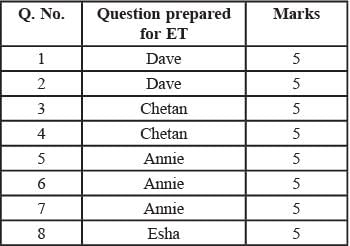
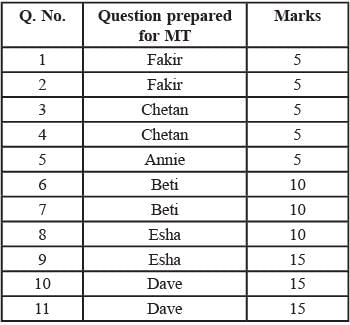
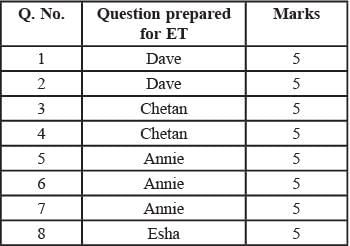
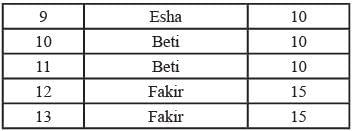
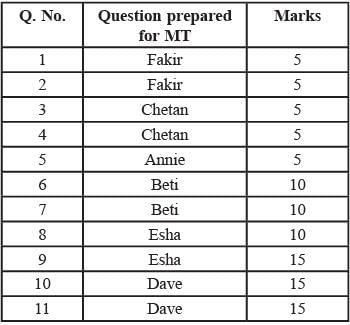
i. Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks.
ii. Annie prepared one question for MT. Every other faculty member prepared more than one questions for MT.
iii. All questions prepared by a faculty member appeared consecutively in MT as well as ET.
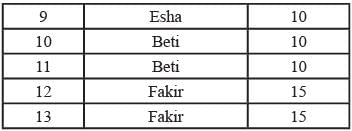
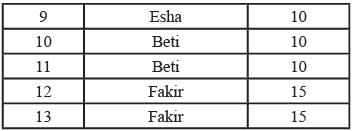
iv. Chelan prepared the third question in both MT and ET: and Esha prepared the eighth question in both.
v. Fakir prepared the first question of MT and the last one in ET. Dave prepared the last question of MT and the first one in ET.
(2019)
Q. The second question in ET was prepared by:
Directions for Questions: The first-year students in a business school are split into six sections. In 2019 the Business Statistics course was taught in these six sections by Annie, Beti, Chetan, Dave, Esha, and Fakir. All six sections had a common midterm (MT) and a common end term (ET) worth 100 marks each. ET contained more questions than MT. Questions for MT and ET were prepared collectively by the six faculty members. Considering MT and ET together, each faculty member prepared the same number of questions.
Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks. In both MT and ET, all the 5-mark questions preceded the 10-mark questions, and all the 15- mark questions followed the 10-mark questions.
The following additional facts are known.
i. Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks.
ii. Annie prepared one question for MT. Every other faculty member prepared more than one questions for MT.
iii. All questions prepared by a faculty member appeared consecutively in MT as well as ET.
iv. Chelan prepared the third question in both MT and ET: and Esha prepared the eighth question in both.
v. Fakir prepared the first question of MT and the last one in ET. Dave prepared the last question of MT and the first one in ET.
(2019)
Q. How many 5-mark questions were there in MT and ET combined?
Directions for Questions: The first-year students in a business school are split into six sections. In 2019 the Business Statistics course was taught in these six sections by Annie, Beti, Chetan, Dave, Esha, and Fakir. All six sections had a common midterm (MT) and a common end term (ET) worth 100 marks each. ET contained more questions than MT. Questions for MT and ET were prepared collectively by the six faculty members. Considering MT and ET together, each faculty member prepared the same number of questions.
Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks. In both MT and ET, all the 5-mark questions preceded the 10-mark questions, and all the 15- mark questions followed the 10-mark questions.
The following additional facts are known.
i. Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks.
ii. Annie prepared one question for MT. Every other faculty member prepared more than one questions for MT.
iii. All questions prepared by a faculty member appeared consecutively in MT as well as ET.
iv. Chelan prepared the third question in both MT and ET: and Esha prepared the eighth question in both.
v. Fakir prepared the first question of MT and the last one in ET. Dave prepared the last question of MT and the first one in ET.
(2019)
Q. Who prepared 15-mark questions for MT and ET?
Directions for Questions: The first-year students in a business school are split into six sections. In 2019 the Business Statistics course was taught in these six sections by Annie, Beti, Chetan, Dave, Esha, and Fakir. All six sections had a common midterm (MT) and a common end term (ET) worth 100 marks each. ET contained more questions than MT. Questions for MT and ET were prepared collectively by the six faculty members. Considering MT and ET together, each faculty member prepared the same number of questions.
Each of MT and ET had at least four questions that were worth 5 marks, at least three questions that were worth 10 marks, and at least two questions that were worth 15 marks. In both MT and ET, all the 5-mark questions preceded the 10-mark questions, and all the 15- mark questions followed the 10-mark questions.
The following additional facts are known.
i. Annie prepared the fifth question for both MT and ET. For MT, this question carried 5 marks.
ii. Annie prepared one question for MT. Every other faculty member prepared more than one questions for MT.
iii. All questions prepared by a faculty member appeared consecutively in MT as well as ET.
iv. Chelan prepared the third question in both MT and ET: and Esha prepared the eighth question in both.
v. Fakir prepared the first question of MT and the last one in ET. Dave prepared the last question of MT and the first one in ET.
(2019)
Q. Which of the following questions did Beti prepare in ET?
Directions for Questions: Students in a college are discussing two proposals -
A: a proposal by the authorities to introduce dress code on campus, and
B: a proposal by the students to allow multinational food franchises to set up outlets on college campus.
A student does not necessarily support either of the two proposals.
In an upcoming election for student union president, there are two candidates in fray: Sunita and Ragini. Every student prefers one of the two candidates.
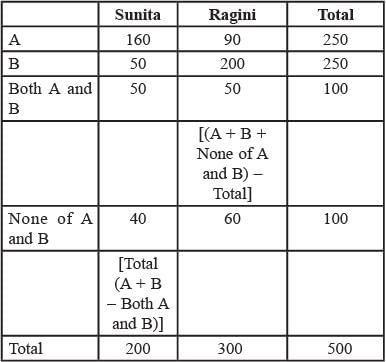
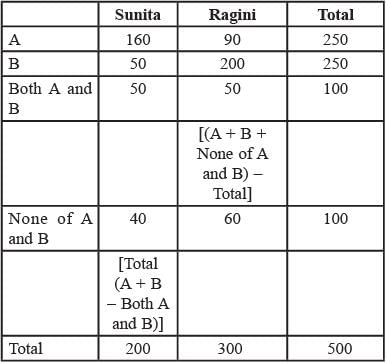
A survey was conducted among the students by picking a sample of 500 students. The following information was noted from this survey.
1. 250 students supported proposal A and 250 students supported proposal B.
2. Among the 200 students who preferred Sunita as student union president. 80% supported proposal A.
3. Among those who preferred Ragini, 30% supported proposal A.
4. 20% of those who supported proposal B preferred Sunita.
5. 40% of those who did not support proposal B preferred Ragini.
6. Every student who preferred Sunita and supported proposal B also supported proposal A.
7. Among those who preferred Ragini, 20% did not support any of the proposals.
(2019)
Q. What percentage of the students surveyed who supported both proposals A and B preferred Sunita as student union president?
Directions for Questions: Students in a college are discussing two proposals -
A: a proposal by the authorities to introduce dress code on campus, and
B: a proposal by the students to allow multinational food franchises to set up outlets on college campus.
A student does not necessarily support either of the two proposals.
In an upcoming election for student union president, there are two candidates in fray: Sunita and Ragini. Every student prefers one of the two candidates.
A survey was conducted among the students by picking a sample of 500 students. The following information was noted from this survey.
1. 250 students supported proposal A and 250 students supported proposal B.
2. Among the 200 students who preferred Sunita as student union president. 80% supported proposal A.
3. Among those who preferred Ragini, 30% supported proposal A.
4. 20% of those who supported proposal B preferred Sunita.
5. 40% of those who did not support proposal B preferred Ragini.
6. Every student who preferred Sunita and supported proposal B also supported proposal A.
7. Among those who preferred Ragini, 20% did not support any of the proposals.
(2019)
Q. How many of the students surveyed supported proposal B, did not support proposal A and preferred Ragini as student union president?
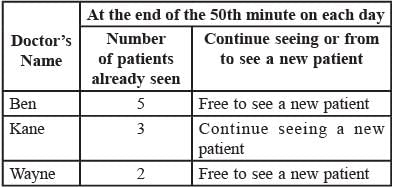
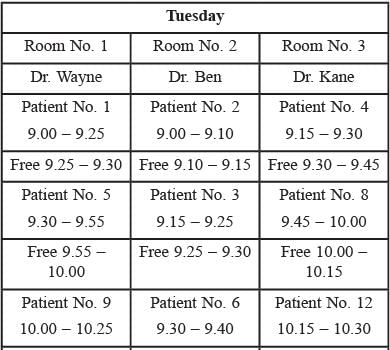
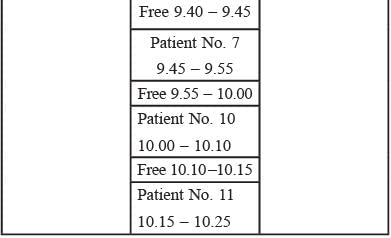
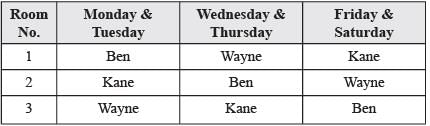
Directions for Questions: Three doctor, Dr. Ben, Dr. Kane and Dr. Wayne visit a particular clinic Monday to Saturday to see patients. Dr. Ben sees each patient for 10 minutes and charges ₹ 100/-, Dr. Kane sees each patient for 15 minutes and charges ₹ 200/-, while Dr. Wayne sees each patient for 25 minutes and charges ₹ 300/-.
The clinic has three rooms numbered 1, 2 and 3 which are assigned to the three doctors as per the following table.
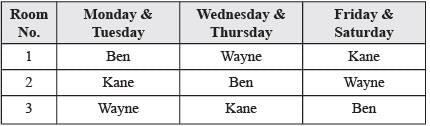
The clinic is open from 9 a.m. to 11.30 a.m. every Monday to Saturday.
On arrival each patient is handed a numbered token indicating their position in the queue, starting with token number 1 every day. As soon as any doctor becomes free, the next patient in the queue enters that emptied room for consultation. If at any time, more than one room is free then the waiting patient enters the room with the smallest number. For example, if the next two patients in the queue have token numbers 7 and 8 and if rooms numbered 1 and 3 are free, then patient with token number 7 enters room number 1 and patient with token number 8 enters room number 3.
(2019)
Q. What is the maximum number of patients that the clinic can cater to on any single day?
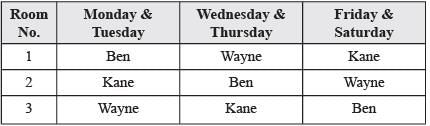
Directions for Questions: Three doctor, Dr. Ben, Dr. Kane and Dr. Wayne visit a particular clinic Monday to Saturday to see patients. Dr. Ben sees each patient for 10 minutes and charges ₹ 100/-, Dr. Kane sees each patient for 15 minutes and charges ₹ 200/-, while Dr. Wayne sees each patient for 25 minutes and charges ₹ 300/-.
The clinic has three rooms numbered 1, 2 and 3 which are assigned to the three doctors as per the following table.
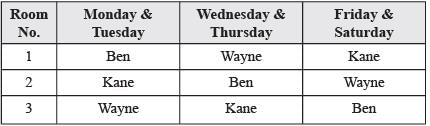
The clinic is open from 9 a.m. to 11.30 a.m. every Monday to Saturday.
On arrival each patient is handed a numbered token indicating their position in the queue, starting with token number 1 every day. As soon as any doctor becomes free, the next patient in the queue enters that emptied room for consultation. If at any time, more than one room is free then the waiting patient enters the room with the smallest number. For example, if the next two patients in the queue have token numbers 7 and 8 and if rooms numbered 1 and 3 are free, then patient with token number 7 enters room number 1 and patient with token number 8 enters room number 3.
(2019)
Q. The queue is never empty on one particular Saturday. Which of the three doctors would earn the maximum amount in consultation charges on that day?
Directions for Questions: Three doctor, Dr. Ben, Dr. Kane and Dr. Wayne visit a particular clinic Monday to Saturday to see patients. Dr. Ben sees each patient for 10 minutes and charges ₹ 100/-, Dr. Kane sees each patient for 15 minutes and charges ₹ 200/-, while Dr. Wayne sees each patient for 25 minutes and charges ₹ 300/-.
The clinic has three rooms numbered 1, 2 and 3 which are assigned to the three doctors as per the following table.
The clinic is open from 9 a.m. to 11.30 a.m. every Monday to Saturday.
On arrival each patient is handed a numbered token indicating their position in the queue, starting with token number 1 every day. As soon as any doctor becomes free, the next patient in the queue enters that emptied room for consultation. If at any time, more than one room is free then the waiting patient enters the room with the smallest number. For example, if the next two patients in the queue have token numbers 7 and 8 and if rooms numbered 1 and 3 are free, then patient with token number 7 enters room number 1 and patient with token number 8 enters room number 3.
(2019)
Q. Mr. Singh visited the clinic on Monday, Wednesday, and Friday of a particular week, arriving at 8:50 a.m. on each of the three days. His token number was 13 on all three days. On which day was he at the clinic for the maximum duration?
Directions for Questions: Three doctor, Dr. Ben, Dr. Kane and Dr. Wayne visit a particular clinic Monday to Saturday to see patients. Dr. Ben sees each patient for 10 minutes and charges ₹ 100/-, Dr. Kane sees each patient for 15 minutes and charges ₹ 200/-, while Dr. Wayne sees each patient for 25 minutes and charges ₹ 300/-.
The clinic has three rooms numbered 1, 2 and 3 which are assigned to the three doctors as per the following table.
The clinic is open from 9 a.m. to 11.30 a.m. every Monday to Saturday.
On arrival each patient is handed a numbered token indicating their position in the queue, starting with token number 1 every day. As soon as any doctor becomes free, the next patient in the queue enters that emptied room for consultation. If at any time, more than one room is free then the waiting patient enters the room with the smallest number. For example, if the next two patients in the queue have token numbers 7 and 8 and if rooms numbered 1 and 3 are free, then patient with token number 7 enters room number 1 and patient with token number 8 enters room number 3.
(2019)
Q. On a slow Thursday, only two patients are waiting at 9 a.m. After that two patients keep arriving at exact 15 minute intervals starting at 9:15 a.m. – i.e. at 9:15 a.m., 9:30 a.m., 9:45 a.m. etc. Then the total duration in minutes when all three doctors are simultaneously free is
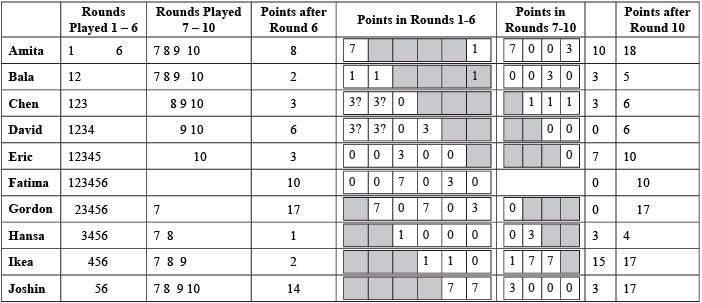
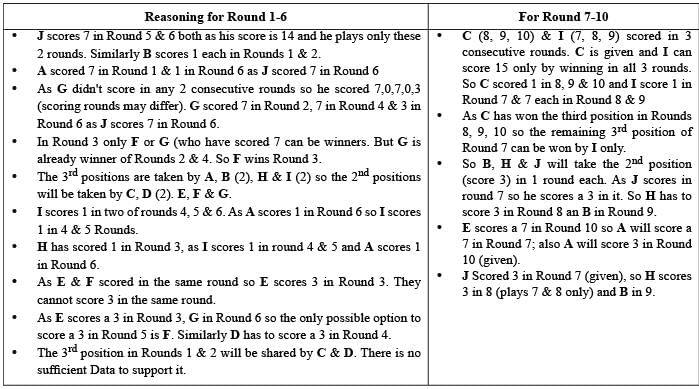
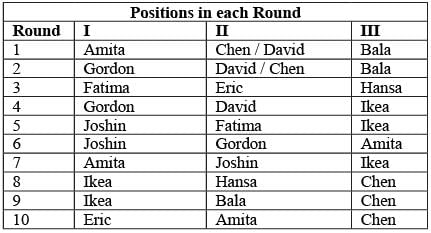
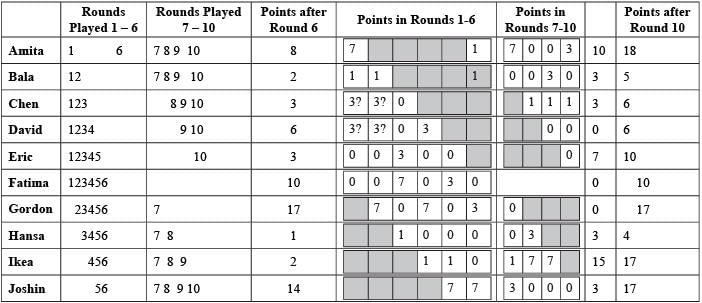
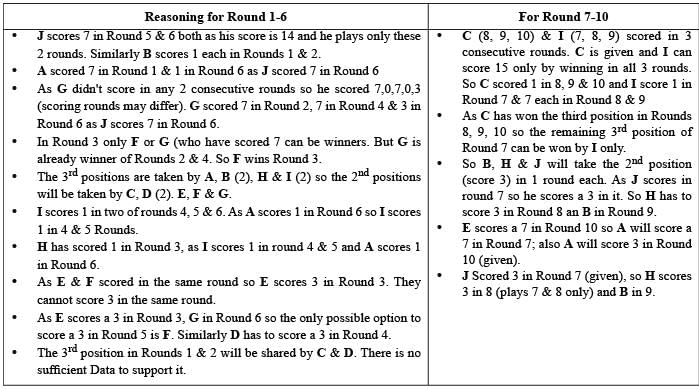
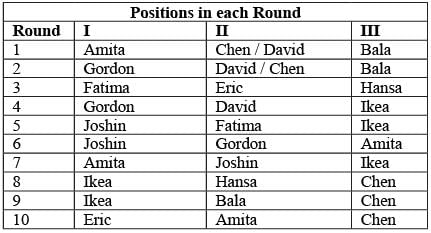
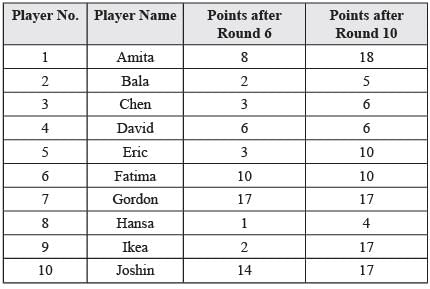
Directions for Questions: Ten players, as listed in the table below, participated in a rifle shooting competition comprising of 10 rounds. Each round had 6 participants. Players numbered 1 through 6 participated in Round 1, players 2 through 7 in Round 2, . . . ., players 5 through 10 in Round 5, players 6 through 10 and 1 in Round 6, players 7 through 10. 1 and 2 in Round 7 and so on.
The top three performances in each round were awarded 7, 3 and 1 points respectively. There were no ties in any of the 10 rounds. The table below gives the total number of points obtained by the 10 players after Round 6 and Round 10.
The following information is known about Rounds 1 through 6:
1. Gordon did not score consecutively in any two rounds.
2. Eric and Fatima both scored in a round.
The following information is known about Rounds 7 through 10:
1. Only two players scored in three consecutive rounds. One of them was Chen. No other player scored in any two consecutive rounds.
2. Joshin scored in Round 7, while Amita scored in Round 10.
3. No player scored in all the four rounds.
(2019)
Q. What were the scores of Chen, David, and Eric respectively after Round 3?
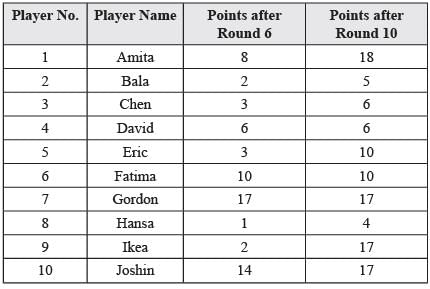
Directions for Questions: Ten players, as listed in the table below, participated in a rifle shooting competition comprising of 10 rounds. Each round had 6 participants. Players numbered 1 through 6 participated in Round 1, players 2 through 7 in Round 2, . . . ., players 5 through 10 in Round 5, players 6 through 10 and 1 in Round 6, players 7 through 10. 1 and 2 in Round 7 and so on.
The top three performances in each round were awarded 7, 3 and 1 points respectively. There were no ties in any of the 10 rounds. The table below gives the total number of points obtained by the 10 players after Round 6 and Round 10.
The following information is known about Rounds 1 through 6:
1. Gordon did not score consecutively in any two rounds.
2. Eric and Fatima both scored in a round.
The following information is known about Rounds 7 through 10:
1. Only two players scored in three consecutive rounds. One of them was Chen. No other player scored in any two consecutive rounds.
2. Joshin scored in Round 7, while Amita scored in Round 10.
3. No player scored in all the four rounds.
(2019)
Q. Which three players were in the last three positions after Round 4?