Probability (Hard Level) - CAT MCQ
10 Questions MCQ Test - Probability (Hard Level)
Out of a pack of 52 cards one is lost; from the re- mainder of the pack, two cards are drawn and are found to be spades. Find the chance that the missing card is a spade.
A pair of fair dice are rolled together till a sum of either 5 or 7 is obtained. The probability that 5 comes before 7 is,
In a bag, there are ten black, eight white and five red balls. Three balls are chosen at random and one is found to be black. The probability that the rest two are white is. Find the probability that the remaining two balls are white.
A bag contains 15 tickets numbered 1 to 15.A Ticket is drawn and replaced. Then one more ticket is drawn and replaced. The probability that first number drawn is even and second is odd is
Three faces of a dice are yellow, two faces are red and one face is blue. The dice is tossed three times.Find the probability that the colours yellow, red and blue appear in the first, second and the third toss respectively:
There are 5 envelopes corresponding to 5 letters. If the letters are placed in the envelopes at random, what is the probability that all the letters are not placed in the right envelopes?
A fair coin is tossed 10 times. Find the probability that two Heads do not occur consecutively.
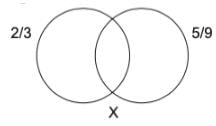
The probability that a contractor will get a plumbing contract is 2/3 and the probability that he will get an electric contract is 5/9. If the probability of getting at least one contract is 4/5, what is the probability that he will get both the contracts?
Two small squares on a chess board are chosen at random. Find the probability that they have a com- mon side:
In a room there are 7 people. The chance that two of them were born on the same day of the week is