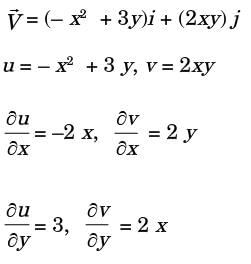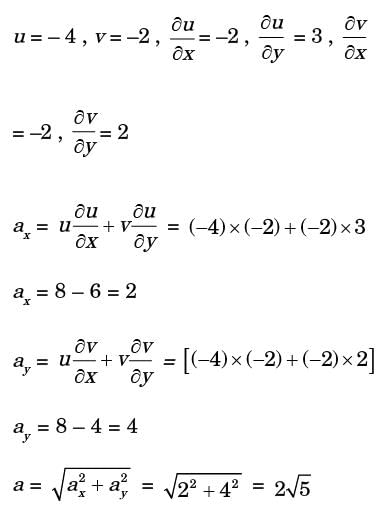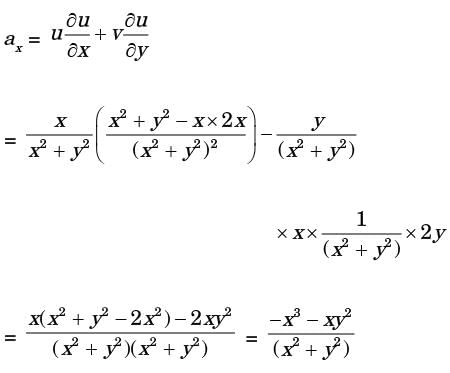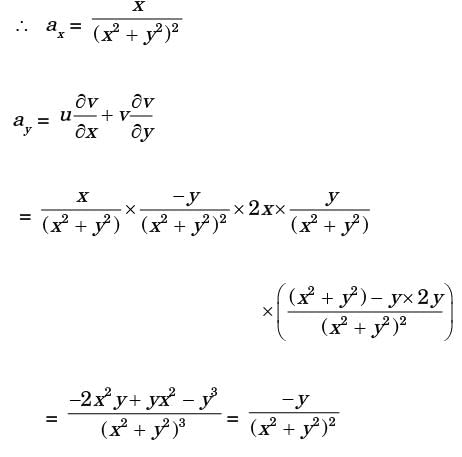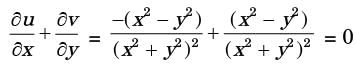Past Year Questions: Fluid Kinematics - Mechanical Engineering MCQ
30 Questions MCQ Test - Past Year Questions: Fluid Kinematics
The stream function in a two dimensional flow field is given by ψ = x2 - y2 The magnitude of the velocity at point (1, 1) is
[1989]
The velocity components in the x and y directions are given by u = λxy3 - x2y, v = xy2 - 3/4y4. The value of λ for a possible flow field involving an incompressible fluid is
[1995]
The velocity components in the x and y directions of a two dimensional potential flow are u and v, respectively. Then ∂u/∂x, is equal to
[2005]
A leaf is caught in a whirlpool. At a given instant, the leaf is at a distance of 120 m from the centre of the whirlpool. The whirlpool can be described by the following velocity distribution:
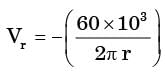 m/s and
m/s and 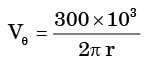 m/s, where r (in meters) is thedistance from the centre of the whirlpool. What will be the distance of the leaf from the centre when it has moved through half a revolution?
m/s, where r (in meters) is thedistance from the centre of the whirlpool. What will be the distance of the leaf from the centre when it has moved through half a revolution?
[2005]
In a steady flow through a nozzle, the flow velocity on the nozzle axis is given by v= u0 (1 + 3x/L)i, where x is the distance along the axis of the nozzle from its inlet plane and L is the length of the nozzle. The time required for a fluid particle on the axis to travel from the inlet to the exit plane of the nozzle is
[2007]
In a two - dimensional velocity field with velocities u and v along the x and y directions respectively, the convective acceleration along the x-direction is given by
[2006]
A flow field which has only convective acceleration is
[2014 Set-4]
Consider the two-dimensional velocity field given by 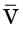 = (5 + a1x + +b1y)
= (5 + a1x + +b1y) 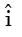 + (4 + a2x + b2y)
+ (4 + a2x + b2y) 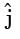 , where a1, b1, a2 and b2 are constants.
, where a1, b1, a2 and b2 are constants.
Which one of the following conditions needs to be satisfied for the flow to be incompressible?
[2017: Set-1]
Streamlines, path lines and streak lines are virtually identical for
[1994]
For a fluid element in a two dimensional flow field (x-y plane), if it will undergo
[1994]
Existence of velocity potential implies that
[1994]
Which combination of the following statements about steady incompressible forced vortex flow is correct?
P : Shear stress is zero at all points in the flow.
Q : Vorticity is zero at all points in the flow.
R : Velocity is directly proportional to the radius from the centre of the vortex.
S : Total mechanical energy per unit mass is constant in the entire flow field.
Select the correct answer using the codes given below:
[2007]
For the continuity equation given by 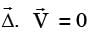 to be valid, where
to be valid, where 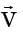 is the velocity vector,which one of the following is a necessary condition?
is the velocity vector,which one of the following is a necessary condition?
[2008]
For an incompressible flow field, V, which one of the following conditions must be satisfied?
[2014, Set-2]
For a two-dimensional incompressible flow field given by 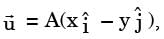 , where A > 0, which one of the following statements is FALSE?
, where A > 0, which one of the following statements is FALSE?
A. It satisfies continuity equation B. It is unidirectional when x → 0 and y → ∞.
C. Its streamlines are given by x = y.
D. It is irrotational
[2018, Set-1]
In a Lagrangian system, the position of a fluid particle in a flow is described as x = x0e–kt and y = y0ekt where t is the time while x0, y0, and k are constants. The flow is
[2018, Set-1]
The velocity potential function for a source varies with the distance r as
[1987]
A streamlined body is defined as a body about which
[1987]
The Newtonian fluid has the following velocity field:

The rate shear deformation ∈yz at the point x = -2, y = -1 and z = 2 for the given flow is
[1988]
In a flow field the stream lines and equipotential lines
[1994]
A fluid flow is represented by the velocity field 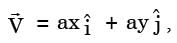 , where a is a constant. The equation of stream line passing through a point (1, 2) is
, where a is a constant. The equation of stream line passing through a point (1, 2) is
[2004]
A two-dimensional flow field has velocities along the x and y directions given by u = x2t and v = –2xyt respectively, where t is time. The equation of streamline is
[2006]
A streamline and an equipotential line in a flow field
[2011]
Consider a velocity field 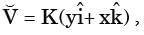 where K is a constant. The vorticity, Ω Z, is
where K is a constant. The vorticity, Ω Z, is
[2014 Set-4]
For a certain two-dimensional incompressible flow, velocity field is given by 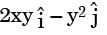 . The streamlines for this flow are given by the family of curves
. The streamlines for this flow are given by the family of curves
[2016,Set-3]
For a steady flow, the velocity field is 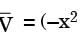
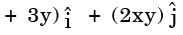 . The magnitude of the acceleration of a particle at (1, - 1) is
. The magnitude of the acceleration of a particle at (1, - 1) is
[2017 Set-1]
A two-dimensional in compressible friction less flow field is given by 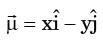 . If ρ is the density of the fluid, the expression for pressure gradient vector at any point in the flow field is given as
. If ρ is the density of the fluid, the expression for pressure gradient vector at any point in the flow field is given as
[2019, Set -2]
For a two-dimensional flow, the velocity field is 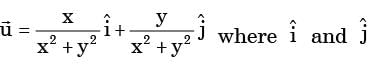 are the basis vectors in the x – y Cartesian coordinate system. Identify the CORRECT statements from below.
are the basis vectors in the x – y Cartesian coordinate system. Identify the CORRECT statements from below.
1. The flow is incompressible
2. The flow is unsteady
3. y-component of acceleration,
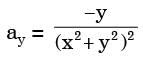
4. x-component of acceleration,
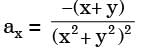
[2016, Set-3]


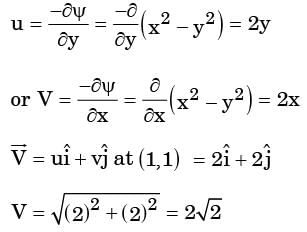
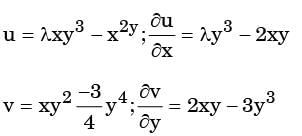
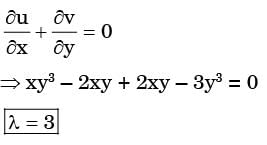

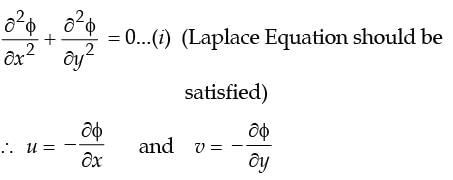
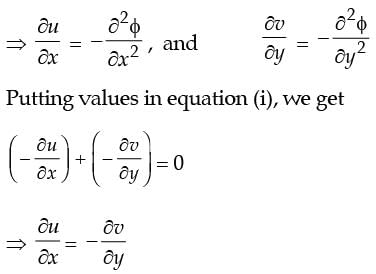
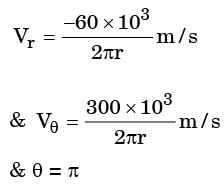
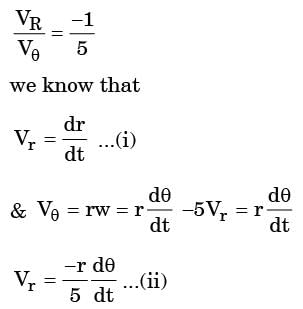
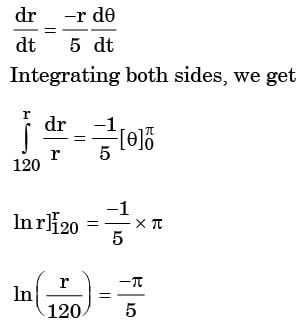
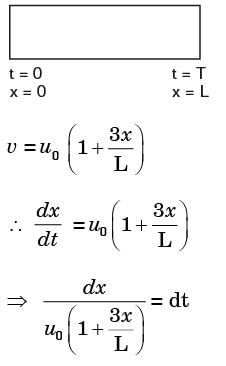
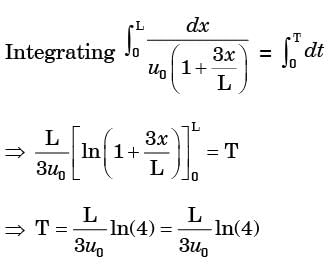
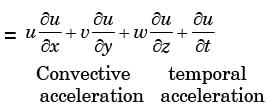
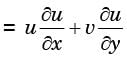
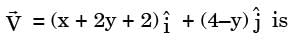
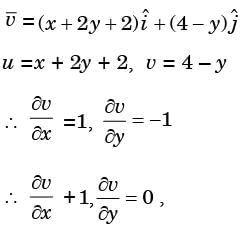
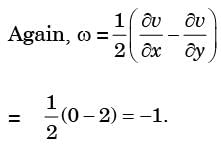
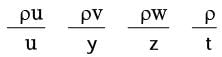
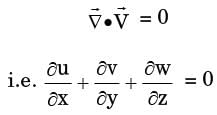


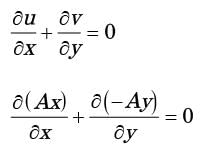
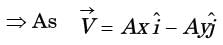
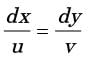



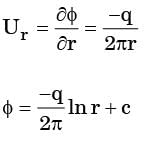
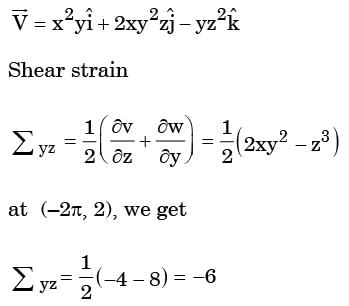
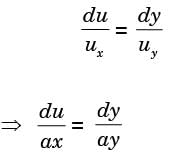
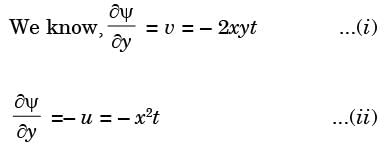 Integrating equation (i), we get
Integrating equation (i), we get
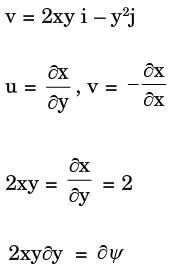
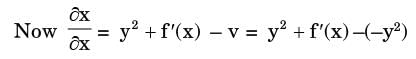 = y1 + f'(x)
= y1 + f'(x)