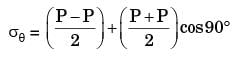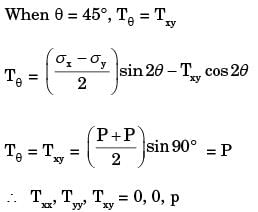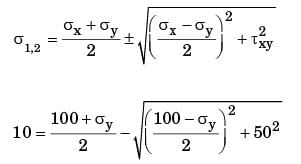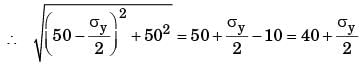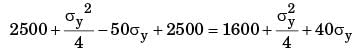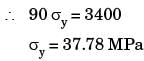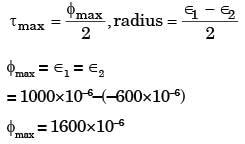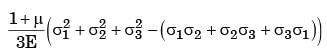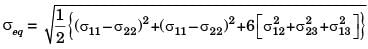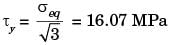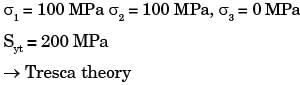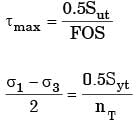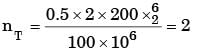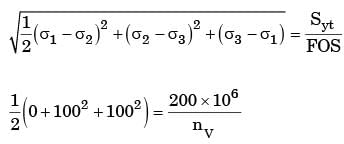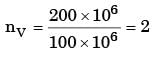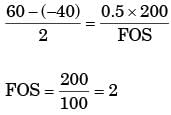Past Year Questions: Principal Stress And Strain - Mechanical Engineering MCQ
16 Questions MCQ Test - Past Year Questions: Principal Stress And Strain
An elastic body is subjected to a tensile stress X in a particular direction and a compressive stress Y in its perpendicular direction. X and Y are unequal in magnitude. On the plane of maximum shear stress in the body there will be
[1989]
The three-dimensional state of stress at a point is given by

The shear stress on the x-face in y-direction at the same point is then equal to
[1990]

The shear stress on the x-face in y-direction at the same point is then equal to
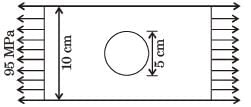
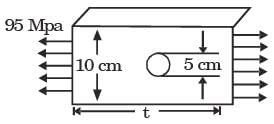
A large uniform plate containing a rivet hole is subjected to uniform uniaxial tension of 95 MPa. The maximum stress in the plate is
[1992]

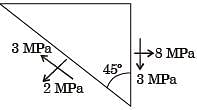
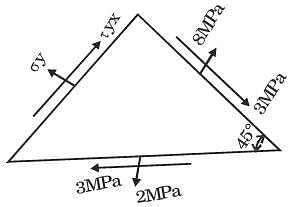
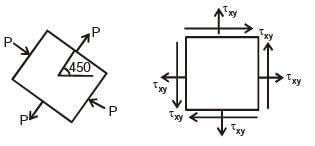
At a point in a stressed body the state of stress on two planes 45° apart is as shown below. Determine the two principal stresses in MPa.
[1993]
A shaft subjected to torsion experiences a pure shear stress x on the surface. The maximum principal stress on the surface which is at 45° to the axis will have a value
[2003]
If the principal stresses in a plane stress problem are σ1 = 100 MPa, σ2 = 40 MPa, the magnitude of the maximum shear stress (in MPa) will be
[2009]
The state of plane-stress at a point is given by σx =200 MPa, σy =100 MPa and τxy = 100 MPa. The maximum shear stress
[2010]
In a plane stress condition, the components of stress at a point are σx = 20 MPa, σy = 80 MPa and σxy = 40 MPa. The maximum shear stress (in MPa) at the point is
[2015]
The state of stress at a point on an element is shown in figure (a). The same state of stress is shown in another coordinate system in figure (b).
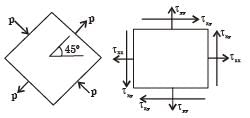
The components (txx, tyy, txy,) are given by
[2016]
The State of stress at a point, for a body in place stress, is shown in the figure below. If the minimum principal stress is 10 kPa, then the normal stress σs (in kPa) is
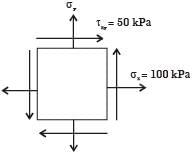
[2018]
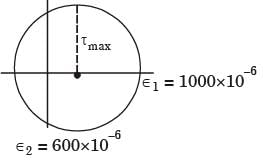
If the two principal strains at a point are 1000 x 10-6 and –600 × 10–6, then the maximum shear strain is
[1996]
According to Von-Mises' distortion energy theory, the distortion energy under three dimensional stress state is represented by
[2006]
Match the following criteria of material failure, under biaxial stresses σ1 and σ2 and yield stress σy, with their corresponding graphic representations:
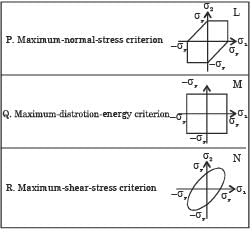
[2011]
The homogenous state of stress for a metal part undergoing plastic deformation is

Where the stress component values are in MPa. Using Von Mises yield criterion, the value of estimated shear yield stress, in MPa is
[2012]
The principal stresses at a point inside a solid object are σ1 = 100 MPa, σ2 = 100 MPa and σ3 = 0 MPa. The yield strength of the material is 200 MPa. The factor of safety calculated using Tresca (maximum shear stress) theory is nT and the factor of safety calculated using Von Mises(maximum distortional energy) theory is nv. Which one of the following relations is TRUE?
[2016]
The principal stresses at a point in a critical -section of a machine component are σ1 = 60 MPa, σ2 = 5 MPa and σ3 = - 40 MPa. For the material of the component, the tensile yield strength is σy = 200 MPa. According to the maximum shear stress theory, the factor of safety is
[2016]


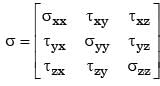

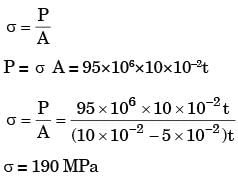
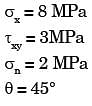
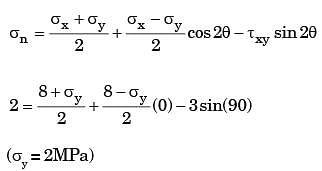

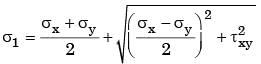
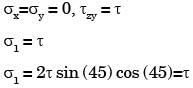
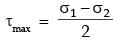
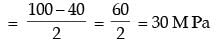
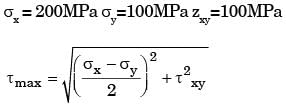
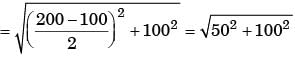
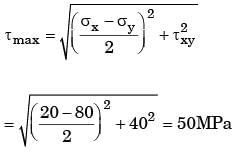
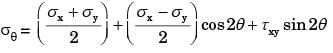
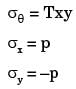
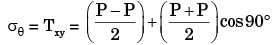 = 0
= 0