Past Year Questions: Queuing Theory And Transportation - Mechanical Engineering MCQ
15 Questions MCQ Test - Past Year Questions: Queuing Theory And Transportation
The cost of providing service in a queuing system increases with
[1997]
At a production machine, parts arrive according to a Poisson process at the rate of 0.35 parts per minute. Processing time for parts have exponential distribution with mean of 2 minutes. What is the probability that a random part arrival finds that there are already 8 parts in the system (in machine + in queue)?
[1999]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a single server infinite population queuing model. Arrivals follow a Poisson distribution with mean 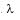 = 4 per hour. The service times are exponential with mean service time equal to 12 minutes. The expected length of the queue will be
= 4 per hour. The service times are exponential with mean service time equal to 12 minutes. The expected length of the queue will be
[2000]
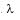 = 4 per hour. The service times are exponential with mean service time equal to 12 minutes. The expected length of the queue will be
= 4 per hour. The service times are exponential with mean service time equal to 12 minutes. The expected length of the queue will beA maintenance service facility has Poisson arrival rates, negative exponential service time and operates on a 'first come first served' queue discipline. Break-downs occur on an average of 3 per day with a range of zero to eight. The maintenance crew can service an average of 6 machines per day with a range of zero to seven.The mean waiting time for an item to be serviced would be
[2004]
Consider a single server queuing model with Poisson arrivals (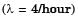 ) and exponential service (
) and exponential service (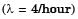 ). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue is
). The number in the system is restricted to a maximum of 10. The probability that a person who comes in leaves without joining the queue is
[2005]
The number of customers arriving at a railway reservation counter is Poisson distributed with an arrival rate of eight customers per hour. The reservation clerk at this counter takes six minutes per customer on an average with an exponentially distributed service time. The average number of the customers in the queue will be
[2006]
In an M/M/1 queuing system, the number of arrivals in an interval of length T is a Poisson random variable i.e. the probability of there being n arrivals in an interval of length T is  The probability density function f(t)of the inter- arrival time is given by
The probability density function f(t)of the inter- arrival time is given by
[2008]
Little's law is a relationship between
[2010]
Cars arrive at a service station according to Poisson's distribution with a mean rate of 5 per hour. The service time per car is exponential with a mean of 10 minutes. At steady state, the average waiting time in the queue is
[2011]
Customers arrive at a ticket counter at a rate of 50 per hr and tickets are issued in the order of their arrival. The average time taken for issuing a ticket is 1 min. Assuming that customer arrivals form a Poisson process and service times are exponentially distributed, the average waiting time in queue in min is
[2013]
For a single server with Poisson arrival and exponential service time, the arrival rate is 12 per hour. Which one of the following service rates will provide a steady state finite queue length?
[2017]
The supply at three sources is 50, 40 and 60 units respectively while the demand at the four destinations is 20, 30,10 and 50 units. In solving this transportation problem.
[2002]
If there are m sources and n destinations in a transportation matrix, the total number of basic variables in a basic feasible solution is
[2014]
The total number of decision variables in the objective function of an assignment problem of size n × n{n jobs and n machines) is
[2014]
A product made in two factories, P and Q, is transported to two destinations, Rand S. The per unit costs of transportation (in Rupees) from factories to destinations are as per the following matrix:Factory P produces 7 units and factory Q produces 9 units of the product. Each destination requires 8 units. If the north-west corner method provides the total transportation cost X(in Rupees) and the optimized (the minimum) total transportation cost is Y(in Rupees), then(X-Y), in Rupees, is
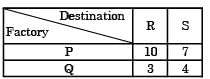
[2017]


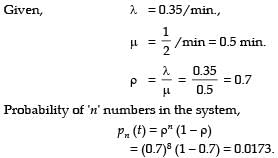
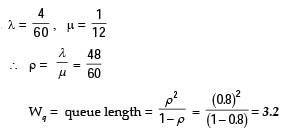
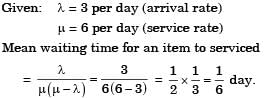
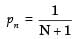



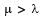 as
as 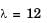 customer s/hour , we need to select option (d)
customer s/hour , we need to select option (d)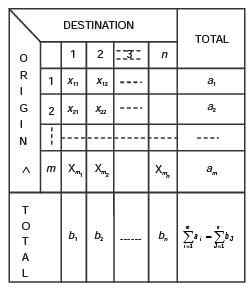
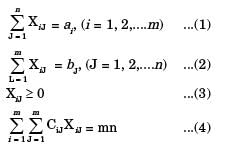 It is evident from the above diagram , that m + n equation s (1) an d (2) constitute m +n – 1 independent equations in mn unknowns.
It is evident from the above diagram , that m + n equation s (1) an d (2) constitute m +n – 1 independent equations in mn unknowns.














