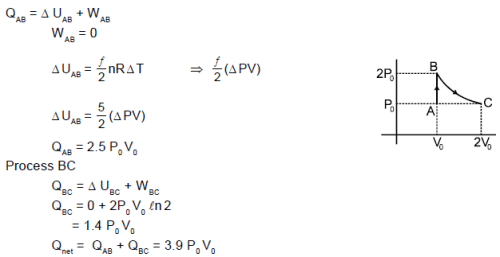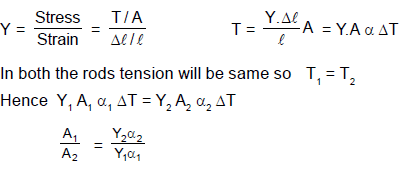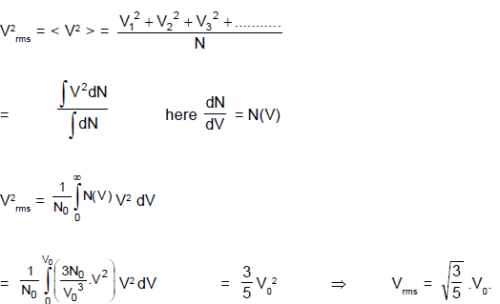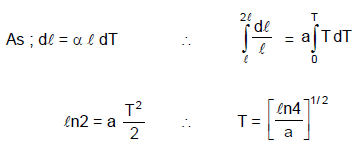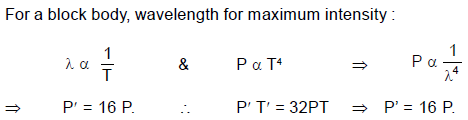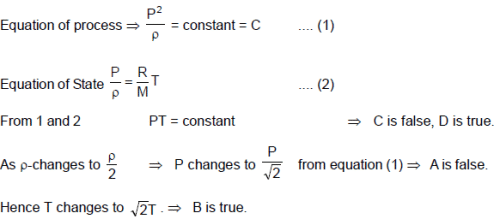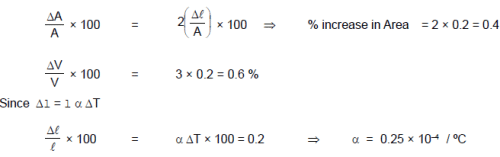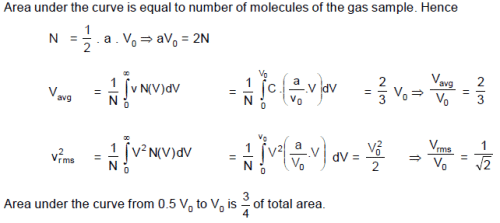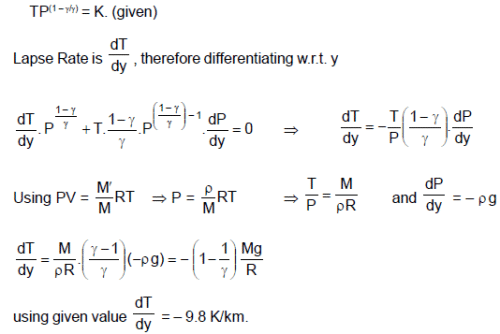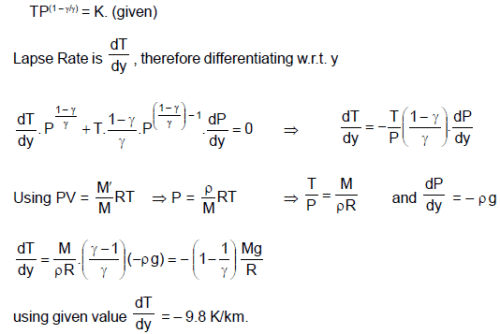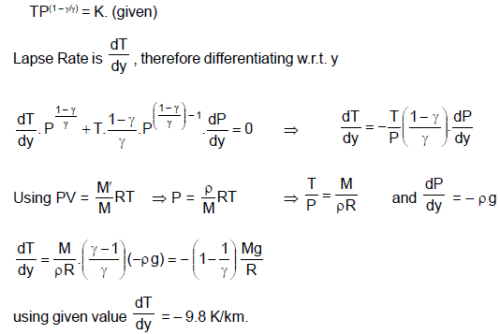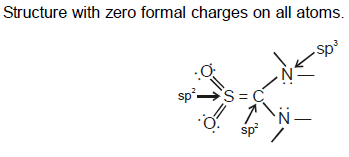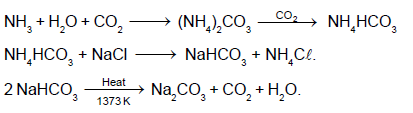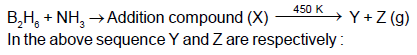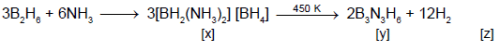JEE Advanced Test- 5 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Test- 5
4 gms of steam at 100°C is added to 20 gms of water at 46°C in a container of negligible mass. Assuming no heat is lost to surrounding, the mass of water in container at thermal equilibrium is. Latent heat of vaporisation = 540 cal/gm. Specific heat of water = 1 cal/gm-°C.
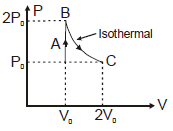
A diatomic ideal gas undergoes a thermodynamic change according to the P–V diagram shown in the figure. The total heat given to the gas is nearly (use ln2 = 0.7) :

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
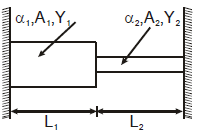
Two rods are joined between fixed supports as shown in the figure. Condition for no change in the lengths of individual rods with the increase of temperature will be ( α1, α2 = linear expansion co-efficient A1, A2 = Area of rods Y1, Y2 = Young modulus )

For a gas sample with N0 number of molecules, function N(V) is given by : N(V) = =
V
V0 and N(V) = 0 for V > V0. Where dN is number of molecules in speed range V to V+ dV. The rms speed of the molecules is :
The co-efficient of thermal expansion of a rod is temperature dependent and is given by the formula α = a T, where a is a positive constant and T in ºC. If the length of the rod is l at temperature 0 ºC, then the temperature at which the length will be 2 l is:
A black body emits radiation at the rate P when its temperature is T. At this temperature the wavelength
at which the radiation has maximum intensity is λ0. If at another temperature T' the power radiated is
P' and wavelength at maximum intensity is then
Thermal coefficient of volume expansion at constant pressure for an ideal gas sample of n moles having pressure P0, volume V0 and temperature T0 is
There are two thin spheres A and B of the same material and same thickness. They emit like black bodies. Radius of A is double that of B. A and B have same temperature T. When A and B are kept in a room of temperature T0 (< T), the ratio of their rates of cooling (rate of fall of temperature) is: [ assume negligible heat exchange between A and B ]
During an experiment, an ideal gas is found to obzey a condition The
gas is initially at temperature T, pressure P and density ρ. The gas expands such that density changes to .
When the temperature of a copper coin is raised by 80 oC, its diameter increases by 0.2%,
Graph shows a hypothetical speed distribution for a sample of N gas particles (for V > V0 ; =0)

STATEMENT–1 : A gas is kept in an insulated cylinder with a movable piston, in compressed state. As the piston is released, temperature of the gas decreases.
STATEMENT–2 : According to the kinetic theory of gas, a molecule colliding with the piston must rebound with less speed than it had before the collision. Hence average speed of the molecules is reduced.
Statement-1 : As the temperature of the blackbody increases, the wavelength at which the spectral intensity (Eλ) is maximum decreases.
Statement-2 : The wavelength at which the spectral intensity will be maximum for a black body is proportional to the fourth power of its absolute temperature.
The atmospheric lapse rate
For small volumes of gas, according to kinetic theory of gases, all parts of the gas are at the same temperature. But for huge volumes of gas like atmosphere, assumption of a uniform temperature throughout the gas is not valid. Different parts of the atmosphere are at different temperatures. Apart from the surface of the earth, variations also occur in temperature at different heights in the atmosphere.
The decrease in temperature with height called the atmospheric lapse rate is similar at various locations across the surface of the Earth. By analyzing the data collected at various locations, it is found that average global lapse rate is – 6.7 °C/Km.
The linear decrease with temperature only occurs in the lower part of the atmosphere called the troposphere. This is the part of the atmosphere in which weather occurs and our planes fly. Above the troposphere is the stratosphere, with an imaginary boundary separating the two layers. In the stratosphere, temperature tends to be relatively constant.
Absorption of sunlight at the Earth’s surface warms the troposphere from below, so vertical convection currents are continually mixing in the air. As a parcel of air rises, its pressure drops and it expands. The parcel does work on its surrounding, so that its internal energy and therefore, its temperature drops. Assume that the vertical mixing is so rapid as to be adiabatic and the quantity TP(1 – λ)/λ has a uniform value through the layers of troposphere.
(M is molecular mass of the air, R is universal gas constant, g is gravitational acc., P and T are pressure and temperature respectively at the point under consideration and y is height.)
Q. If behaviour of the mixing of parcels of air is approximately assumed to be adiabatic then lapse rate can be expressed as :
The atmospheric lapse rate
For small volumes of gas, according to kinetic theory of gases, all parts of the gas are at the same temperature. But for huge volumes of gas like atmosphere, assumption of a uniform temperature throughout the gas is not valid. Different parts of the atmosphere are at different temperatures. Apart from the surface of the earth, variations also occur in temperature at different heights in the atmosphere.
The decrease in temperature with height called the atmospheric lapse rate is similar at various locations across the surface of the Earth. By analyzing the data collected at various locations, it is found that average global lapse rate is – 6.7 °C/Km.
The linear decrease with temperature only occurs in the lower part of the atmosphere called the troposphere. This is the part of the atmosphere in which weather occurs and our planes fly. Above the troposphere is the stratosphere, with an imaginary boundary separating the two layers. In the stratosphere, temperature tends to be relatively constant.
Absorption of sunlight at the Earth’s surface warms the troposphere from below, so vertical convection currents are continually mixing in the air. As a parcel of air rises, its pressure drops and it expands. The parcel does work on its surrounding, so that its internal energy and therefore, its temperature drops. Assume that the vertical mixing is so rapid as to be adiabatic and the quantity TP(1 – λ)/λ has a uniform value through the layers of troposphere.
(M is molecular mass of the air, R is universal gas constant, g is gravitational acc., P and T are pressure and temperature respectively at the point under consideration and y is height.)
Q. Mechanical equilibrium of the atmosphere requires that the pressure decreases with altitude according to . Assuming free fall acceleration to be uniform, then lapse rate is given by
The atmospheric lapse rate
For small volumes of gas, according to kinetic theory of gases, all parts of the gas are at the same temperature. But for huge volumes of gas like atmosphere, assumption of a uniform temperature throughout the gas is not valid. Different parts of the atmosphere are at different temperatures. Apart from the surface of the earth, variations also occur in temperature at different heights in the atmosphere.
The decrease in temperature with height called the atmospheric lapse rate is similar at various locations across the surface of the Earth. By analyzing the data collected at various locations, it is found that average global lapse rate is – 6.7 °C/Km.
The linear decrease with temperature only occurs in the lower part of the atmosphere called the troposphere. This is the part of the atmosphere in which weather occurs and our planes fly. Above the troposphere is the stratosphere, with an imaginary boundary separating the two layers. In the stratosphere, temperature tends to be relatively constant.
Absorption of sunlight at the Earth’s surface warms the troposphere from below, so vertical convection currents are continually mixing in the air. As a parcel of air rises, its pressure drops and it expands. The parcel does work on its surrounding, so that its internal energy and therefore, its temperature drops. Assume that the vertical mixing is so rapid as to be adiabatic and the quantity TP(1 – λ)/λ has a uniform value through the layers of troposphere.
(M is molecular mass of the air, R is universal gas constant, g is gravitational acc., P and T are pressure and temperature respectively at the point under consideration and y is height.)
Q. The value of theoretical lapse rate on the earth is (use g = 9.8 m/s2 ; R = 8.3 J/mol-k and M = 29 g/mol)
The figures given below show different processes (relating pressure P and volume V) for a given amount
of an ideal gas. ΔW is work done by the gas and ΔQ is heat absorbed by the gas.
Column-I Column-II
(A) In Figure (i) (p) ΔQ > 0.
(B) In Figure (ii) (q) ΔW < 0.
(C) In Figure (iii) (r) ΔQ < 0.
(D) In Figure (iv) (for complete cycle) (s) ΔW > 0.
(t) ΔU < 0.
The thermal conductance (reciprocal of the thermal resistance) for axial flow of a truncated cone of length
the radius of the two ends are r1 and r2 assuming that thermal conductivity of the material is K is
. Find the value of n2.
Consider a vertical tube open at both ends. The tube consists of two parts, each of different crosssections
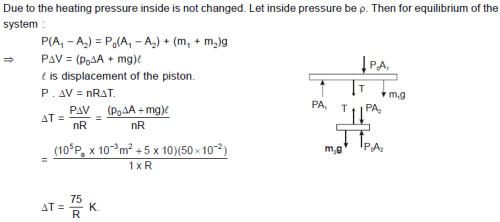
and each part having a piston which can move smoothly in respective tubes. The two pistons are joined together by an inextensible wire. The combined mass of the two piston is 5 kg and area of cross-section of the upper piston is 10 cm2 greater than that of the lower piston. Amount of gas enclosed by the pistons is one mole. When the gas is heated slowly, pistons move by 50 cm. Find rise in the temperature of the gas, in the form (X/R) K where R is universal gas constant. Use g = 10 m/s2 and outside pressure = 105N/m2). Fill value of X in the answer sheet.
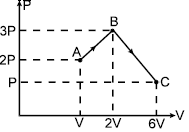
One mole of monoatomic ideal gas undergoes a process ABC as shown in figure. The maximum temperature of the gas during the process ABC is in the form . Find X.
One mole of an ideal gas is kept enclosed under a light piston (area=10-2m2) connected by a compressed
spring (spring constant 200 N/m). The volume of gas is 0.83 m3 and its temperature is 100K. The gas
is heated so that it compresses the spring further by 0.1 m. Find the work done by the gas in the
process in joules ? (Take R = 8.3 J/K-mole and suppose there is no atmosphere).
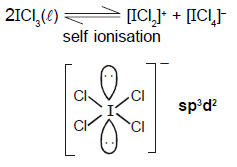
The hybridisation and geometry of the anion of ICl3 in liquid phase is :
Based on the Valence Shell Electron Pair Repulsion (VSEPR) model, what is the geometry around the sulphur, carbon and nitrogen in the thiourea – S , S – dioxide, O2SC(NH2)2 ? (consider the Lewis structure with zero formal charges on all atoms).
The following flow diagram represents the manufacturing of sodium carbonate
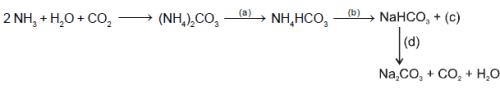
Which of the following options describes the reagents, products and reaction conditions (given in parentheses)?
When boron is fused with potassium hydroxide which pair of species are formed ?
Orthosilicate ions,(SiO44-) undergo polycondensation to forms pyrosilicate, [O3Si – O – SiO3]6-, in presence
of :