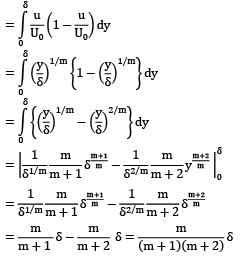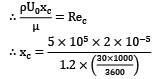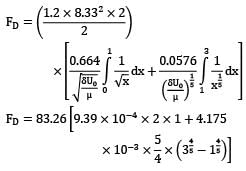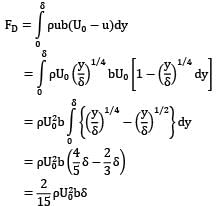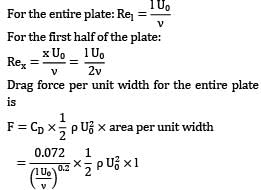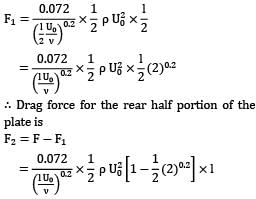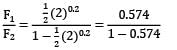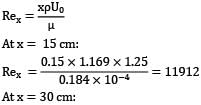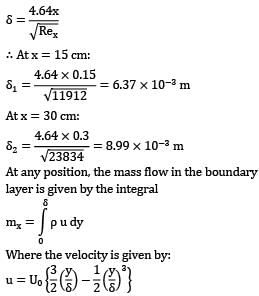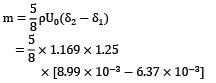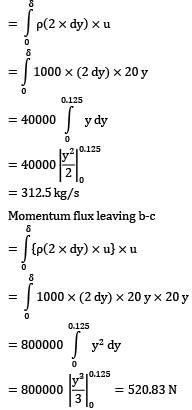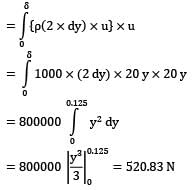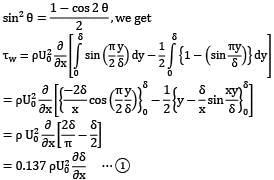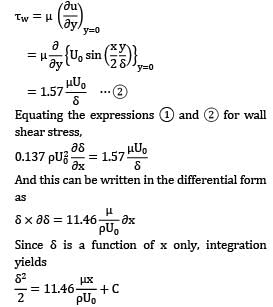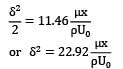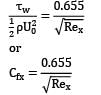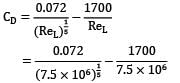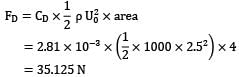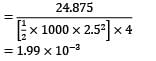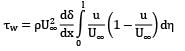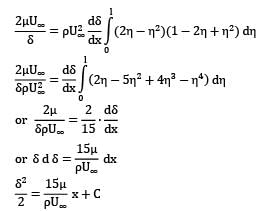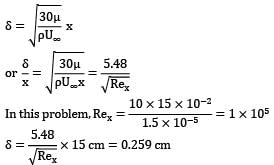Test: Boundary Layer Level - 3 - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Boundary Layer Level - 3
Determine the displacement thickness and momentum thickness in terms of the nominal boundary layer thickness δ in respect of the following velocity profiles in the boundary layer on a flat plate.
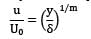
Where u is the velocity at a height y above the surface and U0 is the free stream velocity.
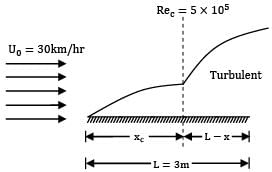
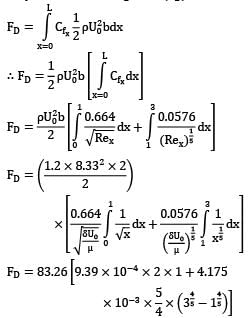
Consider a two seater car that moves with a speed of 30 km/hr. Predict the drag force on the car treating it as a flat surface of 3.0 × 2.0 given, density of air (δ) = 1.2 kg/m3
dynamic viscosity of air = 2 × 10−5 kg/m‑sec.
Critical Reynolds number for transition of boundary layer from laminar to turbulent = 5 × 10
Local skin friction coefficient (Cfx)
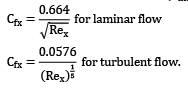
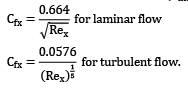
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A roughened thin board 25 cm wide 200 cm long moves at 3 m⁄s through water. The boundary layer is 5 cm thick on both sides at rear end of the board and the velocity distribution is prescribed by the relation:

Find the drag force in Newton.
A flat plate was positioned at zero incidence in a uniform flow stream of air. Assuming the boundary layer to be turbulent over the entire plate, work out the ratio of skin-friction drag forces on the front and rear half part of the plate. (Upto 2 decimal places) For turbulent boundary layer, the average drag coefficient CD is prescribed by the relation:
![]()
Air at 25°C and 1 bar flows over a flat plate at a speed of 1.25 m/s. Consider the sections at a distance of 15 cm and 30 cm and from the leading edge of the plate. What would be the mass entrainment (mass flow exiting the boundary layer) between these two sections? Assume parabolic velocity distribution.
![]()
The viscosity of air at 25°C is stated to be 6.62 × 10−2 kg ⁄ hr -m. Give your answer in kg/hr.
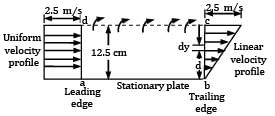
Water flows past a flat plate, 5 m × 2 m, kept parallel to flow direction. The flow velocity ahead of the plate is uniform and has a value of 2.5 m⁄s. At the trailing edge, the velocity increases linearly from zero at the plate to 2.5 m⁄s at a transverse distance of 12.5 cm from it. Assuming that pressure is uniform everywhere in the flow fluid.
Calculate the drag force on the plate.
Refer Fig. for the flow past stationary plate.
The velocity distribution in the boundary layer of a flat plate is prescribed by the relation
![]()
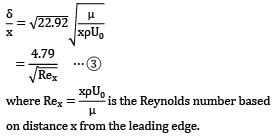
Use momentum integral equation to develop an expression for boundary layer thickness, and local skin friction coefficient, in terms of Reynolds number.
Apart from frictional drag a ship or submarine experiences a wave drag as well and similar to skin-friction coefficient, a wave drag coefficient is defined.
The length of the model of a submarine is 3 m and its wetted surface area is 4 m2 . When it is towed in fresh water at 2.5 m/s, it experiences a total drag of 60 N. Make calculations for the average wave drag coefficient.
For fresh water: ρ = 1000 kg/m3 and ν = 1 × 10−6 m2/s In case, the boundary layer at trailing edge is turbulent, the average drag coefficient is given as
![]()
(Multiply your answer by 1000 and give the value).
Water flows over a flat plate at a free stream velocity of 0.15 m⁄s . There is no pressure gradient and laminar boundary layer is 6 mm thick. Assume a sinusoidal velocity profile
![]()
For the flow conditions stated above, calculate the local wall shear stress and skin friction coefficient.
Air moves over a flat plate with a uniform free stream velocity of 10 m/s. At a position 15 cm away from the front edge of the plate, what is the boundary layer thickness? Use a parabolic profile in the boundary layer. For air, ν = 1.5 × 10−5 m2/s and ρ = 1.23 kg/m3. Give your answer in mm.