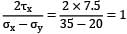Test: Analysis of Stress & Strain Level - 2 - Mechanical Engineering MCQ

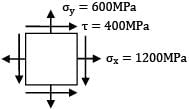
A body is subjected to a tensile stress of 1200 MPa on one plane and another tensile stress of 600 MPa on a plane at right angles to the former. If is also subjected to shear stress of 400 MPa on the same planes. The maximum shear stress will be

A Plane stressed element is subjected to the state of stress given by σ_x = τ_xy = 100 kgf/cm² and σ_y = 0. Maximum shear stress in the element is equal to

The radius of Mohr’s circle for two unlike principal stresses of magnitude σ is

At a point in a stressed material, the stress system is σ_x = + 800N/mm² , σ_y = 0 and q = 0.

The radius of the Mohr’s stress circle for this case is__________ units.

The principal stresses at a point are 150.0 MPa and − 50.0 MPa; the radius of the corresponding Mohr’s circle will be

A spherical ball of volume 10⁶ mm³ is subjected to a hydrostatic pressure of 90 MPa. If the bulk modulus for the material is 180 GPa, the change in the volume of the ball is

An element is subjected to p_x = 35 MPa, p_y = 20 MPa and shear stress q = 7.5 MPa. Then the direction of principal stresses is

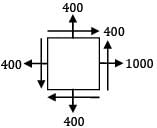
For an inclined plane in a rectangular block subjected to two mutually perpendicular normal stresses 1000 MPa and 400 MPa and shear stress 400 MPa, the maximum normal stress will be

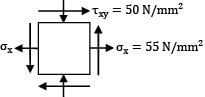
The normal stresses of 55 N/mm² tensile and 45 N/mm² compressive on two mutually perpendicular planes are acting at a point in a piece of elastic material. These planes also carry shear stress of 50 N/mm². The minor principal stress will be

A rectangular strain rosette, shown in figure give following reading in a strain measurement task ϵ_P = 100 × 10⁻⁶, ϵ_Q = 150 × 10⁻⁶, ϵR = 200 × 10⁻⁶. The major principal strain is

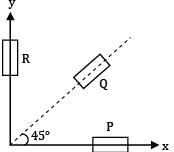
If major and minor principal strains are given as 500 × 10⁻⁶ and − 200 × 10⁻⁶. Then calculate the maximum shear strain.

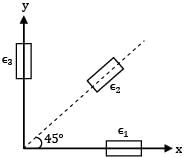
A rectangular strain rosette, shown in figure gives following reading in a strain measurement task ϵ₁ = 1000 × 10⁻⁶, ϵ₂ = 800 × 10⁻⁶ and ϵ₃ = 600 × 10⁻⁶. The direction of the major principal strain with respect to gauge 1 is

Consider the following failure criteria and match them with their corresponding graphical representations.

P - Maximum principal stress Theory

Q - Maximum distortion energy Theory

R - Maximum principal strain Theory

I.

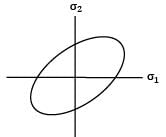
II.

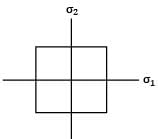
III.

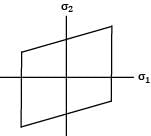
Common Data for Question No: 17 and 18 If the principal stress at a point in an elastic material are 2σ, σ and − σ/2 the properties are S_yt = 200 MPa and μ = 0.3

The value of σ at failure according to maximum principal stress theory

The value of σ at failure according to strain energy theory

A spherical pressure shell 3.8 meters diameter and 3 mm thick is subjected to an internal pressure ‘P’. The elastic limit of the shell material in simple tension is 260 MPa. The factor of safety is to 2.8. The internal pressure, if the failure of shell is to be prevented, according to maximum shear stress theory is

The force acting on a bolt consists of two components, an axial pull of 14 kN and a transverse shear load of 7 kN. The bolt material yield strength is 340 MPa and the factor of safety is 3 then, the cross sectional area of bolt required according to maximum shear stress theory is