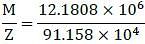Test: Stresses in Beams Level - 2 - Mechanical Engineering MCQ
20 Questions MCQ Test - Test: Stresses in Beams Level - 2
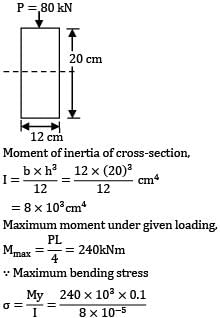
A beam of rectangular section (12cm wide × 20cm deep) is simply supported over a span of 12m. It is acted upon by a concentrated load of 80 kN at the mid span. The maximum bending stress induced is
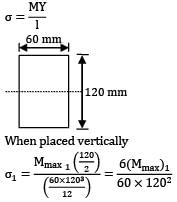
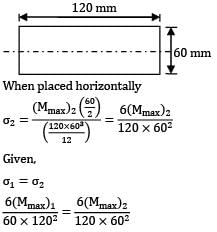
A beam with a rectangular section 120mm × 60mm, designed to be placed vertically is placed horizontally by mistake. The maximum stress is to be limited, the reduction in load carrying capacity would be
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
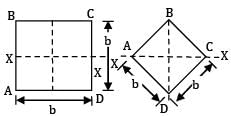
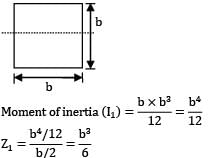
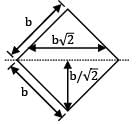
The ratio of the section moduli of a square beam (Z) when square section is placed
(i) With two sides horizontal (Z1 ) and
(ii) With a diagonal horizontal (Z2 ) as shown is

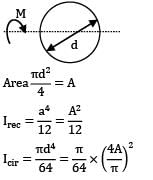
Two beams, one having a square cross-section and another circular cross-section, are subjected to the same amount of bending moment. If the cross-sectional area as well as the material of both the beams are the same, then
1. Both the beams will experience the same amount of deformation
2. The circular beam experience more extreme flexural stress than the square one
Which of the above is/are correct?
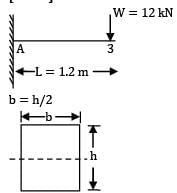
A cantilever of length 1.2m carries a concentrated load of 12kN at the free end. The beam is of rectangular cross-section with breadth equal to half the depth. The maximum stress due to bending is not to exceed 100 N/mm2. The minimum depth of the beam should be
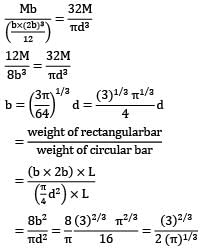
A bar of rectangular cross-section (b × 2b) and another bar of circular cross-section (diameter = d) with the same length, are made of same material, and are subjected to the same bending moment and have the same maximum bending stress developed. The ratio of weights of rectangular bar and circular bar will be
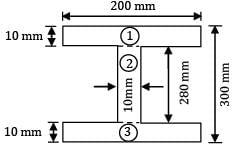
An equal flange I-section of 300mm depth and 200mm wide flanges has a uniform thickness of 10mm. it is subjected to a bending moment of 100kN-m. The bending stress at top most fiber is (in MPa)
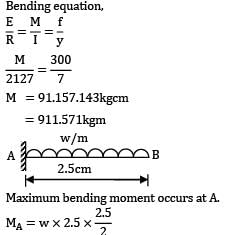
A cantilever has length of 2.5cm. It is of T section with IX = 2127cm4 and fibre distance (tensile) from neutral axis is 7cm. if the maximum allowable tensile stress is 300kgf/sq cm. Then the maximum UDL that can be applied in kg/cm is
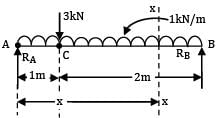
A beam AB simply supported at its ends A and B, 3m long, carries a uniformly distributed load of 1kN/m over its entire length and a concentrated load of 3kN, at 1m from A.
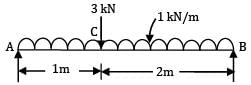
If ISMB 150 with IXX = 300 cm4 is used for the beam, the maximum value of bending stress is
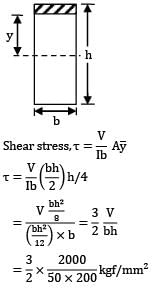
The maximum shearing stress induced in the beam section at any layer at any position along the beam length (shown in figure) is equal to
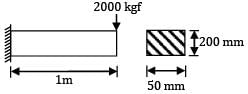
Cross-section of beam
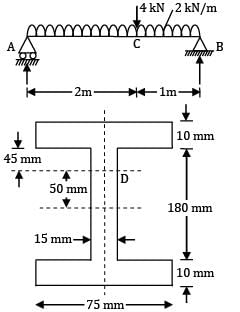
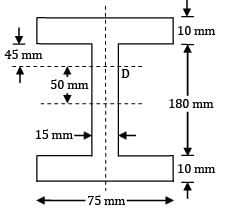
Simply supported beam of 3m span is subjected to loads as shown in figure below the beam is of I-section and all of the dimensions are in mm. The maximum compressive stress at point D in the web is (The section is located at a distance of 1m for right hand support)
Two beams of equal cross-section area are subjected to equal bending moment. If one beam has square cross-section and the other has circular section, then
A simply supported beam of span L and constant width b carries a point load W at mid-span. The depth of the beam required at the mid span for maximum extreme fiber stress P.
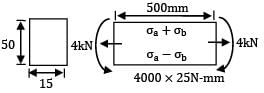
A link is under a pull which lies on one of the faces as shown in the figure below. The magnitude of maximum compressive stress in the link would be

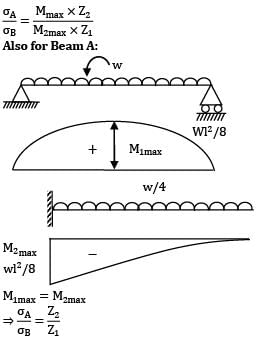
Beam A is simply supported at its end and carries UDL of intensity ‘w’ over its entire length. It is made of steel having Young’s Modulus E. Beam B is cantilever and carries a UDL of intensity w/4 over its length. It is made of brass having young’s modulus E/2. The two beams are of the same length and have the same cross-sectional area. If σA and σB denote the maximum bending stresses developed in beams A and B, respectively, then which one of the following is correct?
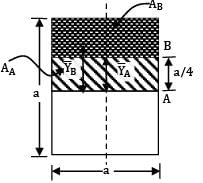
At a section of a beam, shear force is F with zero BM. The cross-section is square with side ‘a’. Point ! lies on the neutral axis and point B is mid-way between the neutral axis and top edge, i.e. at distance a/4 above the neutral axis. If τA and τB denote shear stresses at points A and B, then what is the value of τA⁄τB?
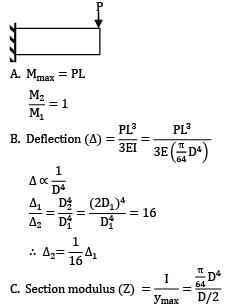
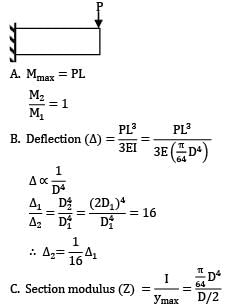
If the area of cross-section of a circular section beam is made four times, keeping the loads, length, support conditions and material of the beam unchanged, then the quantities (List-I) will change through different factors (List-II). Match the List-I with the List-II and select the correct answer using the code given below the lists.
List-I List-II
a. Maximum BM 1. 8
b. Deflection 2. 1
c. Bending Stress 3. 1/8
d. Section Modulus 4. 1/16
Codes: a b c d
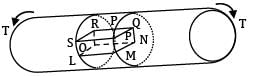
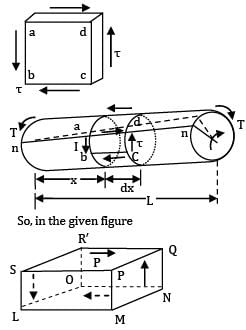
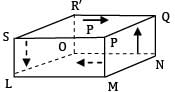
A shaft is subjected to torsion as shown in the figure below.
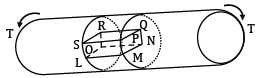
Which of the following figures represents the shear stress on the element LMNOPQRS?
Shear stress
A cast iron water pipe 300 mm outer diameter with 15 mm wall thickness is supported over a span of 8 m. The maximum stress in cast iron when the pipe is running full of water is ___________MPa.
Take Density of CI = 71.6 kN/m3, Density of water = 9.8 kN/m3
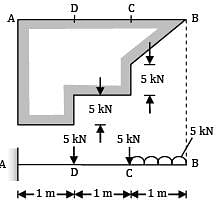
The shear force diagram for rectangular cross section beam is shown in the figure below. Width of the beam in 100 mm and depth is 250 mm, the maximum bending stress in the beam is ___________ MPa.


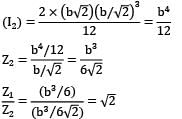
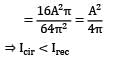
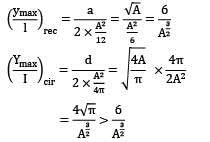
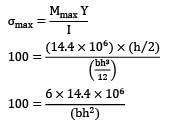
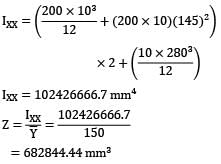
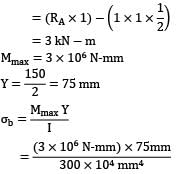
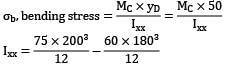
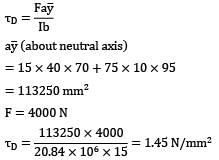

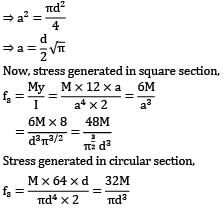
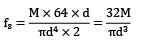
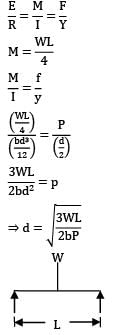
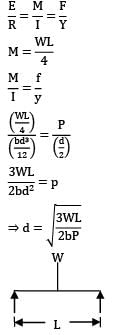

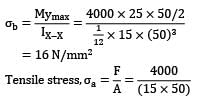
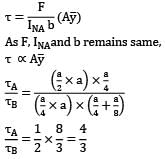
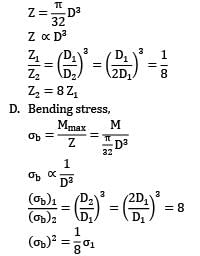
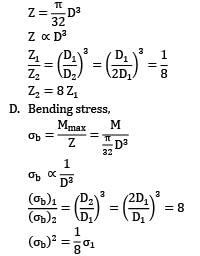

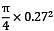 = 0.05725 m2
= 0.05725 m2