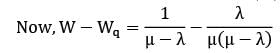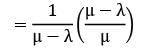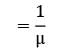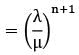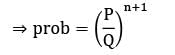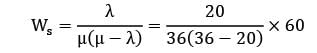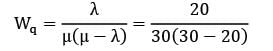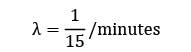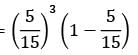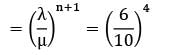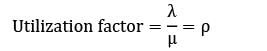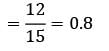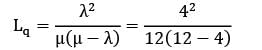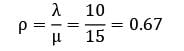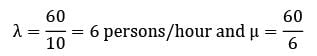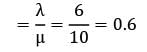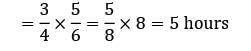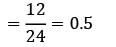Test: Queueing Theory Level - 1 - Mechanical Engineering MCQ

Which of the following term is not related to queueing?

In a M/M/1 queueing system, the expected waiting time of a unit that actually waits is given by

The expected waiting time in the system is

In a single server queue customers are served at a rate of μ. If W and Wq represent the mean waiting time in the system and mean waiting time in the queue respectively, then W will be equal to

In a queueing model, P is the mean arrival rate and Q is the mean service rate. The probability that the queue length is greater than n is

Which of the following represents traffic intensity?

In single server queueing model if arrival rate is λ and service rate is μ, then what is the probability of the system being idle?

A garage is manned with a single worker. Customers arrive at a rate of 20 per hour. The time required to provide service is exponentially distributed with a mean of 100 seconds. The mean waiting time (in minutes) of a customer, needing repair facility in the queue will be __________

A machine receives jobs at a rate of 20 per hour and the processing rate is 30 per hour. How much time (in minutes) on an average does a job have to wait before it gets loaded on to the machine?

Trains arrive at a yard every 15 minutes and the service time is 5 minutes. The probability that the yard has 3 trains in the system is __________

Consider the following data arrival rate = 6 per hour, departure rate = 10 per hour The probability that queue size is greater than 3 is

In a health clinic, the average rate of arrival of patients is 12 per hour. On an average, a doctor can serve patients at the rate of one patient every four minutes. Find the utilization factor.

In a M/M/1: FCFS/∞/∞ queueing system the mean arrival rates is 4/hour and mean service rate is 12/hour. The expected length of nonempty queue is

If the arrivals at a service facility are distributed as per the poisson distribution with a mean rate of 10 per hour and the services are exponentially distributed with a mean service time of 4 minutes, what is the probability that a customer may have to wait to be served?

The inter-arrival times at a tool crib are exponential with an average time of 10 minutes and the length of the service time is assumed to be exponential with mean 6 minutes. The probability that a person arriving at the booth will have to wait is equal to

In a single server queueing model the mean arrival rate is 6 per shift of (8 hours) and the arrival follows poisson distribution. The mean service time is 50 minutes and it follows exponential distribution. The working time of the server is (hours)

Customers arrive at a ticket counter with an arrival rate of 12 customers per hour. A clerk serves the customers at a rate of 24 per hour. The probability that the clerk is busy is __________