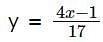Test: Inequalities- 1 - CAT MCQ
10 Questions MCQ Test - Test: Inequalities- 1
Let a, b, c, d be four integers such that a + b + c + d = 4m + 1 where m is a positive integer. Given m, which one of the following is necessarily true?
If x > 5 and y < -1, then which of the following statements is true?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If a, b, c and d are four positive real numbers such that abcd = 1, what is the minimum value of (1 + a)(1 + b)(1 + c)(1+ d)?
If x, y and z are real numbers such that x + y + z = 5 and xy + yz + zx = 3, what is the largest value that x can have?
The number of integers n satisfying -n + 2 ≥ 0 and 2n ≥ 4 is
x, y and z are three positive integers such that x > y > z. Which of the following is closest to the product xyz?
For x = 15, y = 10 and z = 9, find the value of le(x, min(y, x-z), le(9, 8, ma(x, y, z)).
The number of positive integer valued pairs (x, y), satisfying 4x – 17 y = 1 and x < 1000 is:
p, q and r are three non-negative integers such that p + q + r = 10. The maximum value of pq + qr + pr + pqr is