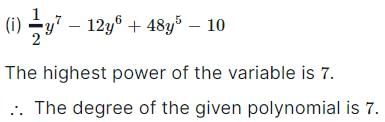Test: Polynomials (Easy) - Class 10 MCQ
15 Questions MCQ Test - Test: Polynomials (Easy)
Write down the degree of following polynomials in x: 3 - 2x
Find the degree of the given algebraic expression ax2 + bx + c
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If x = 2 and x = 3 are zeroes of the quadratic polynomial x2 + ax + b, the values of a and b respectively are
Write the degree of each of the following polynomials: 1 / 2y7 - 12y6 + 48y5 - 10
Let p(x) = ax2 + bx + c be a quadratic polynomial. It can have at most
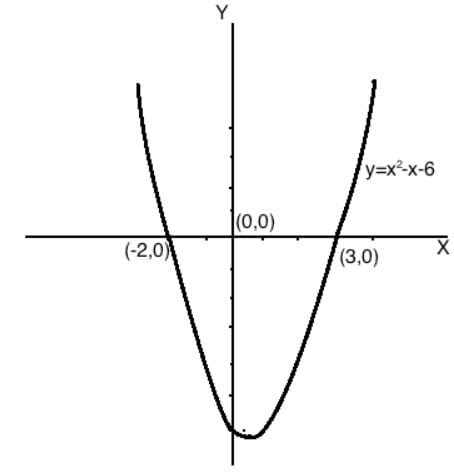
Draw the graphs of y = x2 - x - 6 and find the zeroes in each case.
Assertion: Degree of a zero polynomial is not defined.
Reason: Degree of a non-zero constant polynomial is 0
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively: 0, 3
Find the zero of the polynomial in each of the following in the following case: p(x) = x +
5
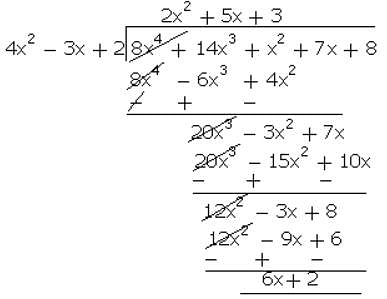
What must be subtracted from the polynomial 8x4 + 14x3 + x2 + 7x + 8 so that the resulting polynomial is exactly divisible by 4x2 - 3x + 2?
Classify the following polynomial based on their degree: 3x2 + 2x + 1