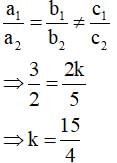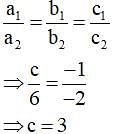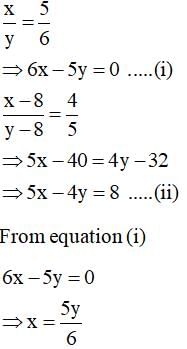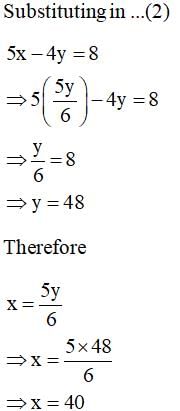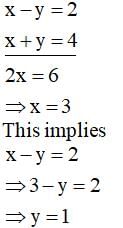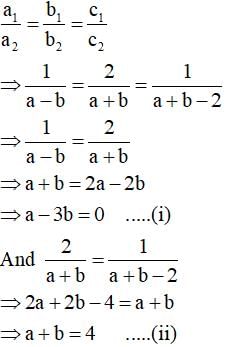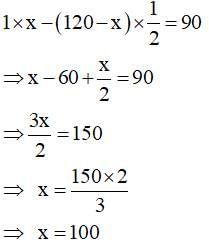All Courses
Get the App Signup / Login
Sign in Open App
Class 10 Exam  >  Class 10 Tests  >  Test: Pair of Linear Equations in Two Variables (Medium) - Class 10 MCQ

Test: Pair of Linear Equations in Two Variables (Medium) - Class 10 MCQ


Test Description

19 Questions MCQ Test - Test: Pair of Linear Equations in Two Variables (Medium)

Test: Pair of Linear Equations in Two Variables (Medium) for Class 10 2024 is part of Class 10 preparation. The Test: Pair of Linear Equations in Two Variables (Medium) questions and answers have been prepared according to the Class 10 exam syllabus.The Test: Pair of Linear Equations in Two Variables (Medium) MCQs are made for Class 10 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Pair of Linear Equations in Two Variables (Medium) below.
Solutions of Test: Pair of Linear Equations in Two Variables (Medium) questions in English are available as part of our course for Class 10 & Test: Pair of Linear Equations in Two Variables (Medium) solutions in Hindi for Class 10 course. Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free. Attempt Test: Pair of Linear Equations in Two Variables (Medium) | 19 questions in 20 minutes | Mock test for Class 10 preparation | Free important questions MCQ to study for Class 10 Exam | Download free PDF with solutions
Test: Pair of Linear Equations in Two Variables (Medium) - Question 1
Save

If the lines given by

3x + 2ky = 2

2x + 5y + 1 = 0

are parallel, then the value of k is

Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 1
For parallel lines

Test: Pair of Linear Equations in Two Variables (Medium) - Question 2
Save

The value of c for which the pair of equations cx – y = 2 and 6x – 2y = 3 will have infinitely many solutions is

Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 2

For infinitely many solutions

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Pair of Linear Equations in Two Variables (Medium) - Question 3
Save

Solve for x and y, if x + y = 7and 2x + 3y = 18.

Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 3
2x + 3y = 18 .......... (1)

x + y = 7 ......... (2)

Multiplying equation (2) by 2, we get

2x + 2y = 14 ........ (3)

Subtracting (3) from (2), we get

y = 4

Using this in x + y = 7, we have

x + 4 = 7

or x = 7 − 4 = 3

Test: Pair of Linear Equations in Two Variables (Medium) - Question 4
Save

One equation of a pair of dependent linear equations is –5x + 7y – 2 = 0. The second equation can be
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 4
For dependent pair, the two lines must have

a1 / a2 = b1 / b2 = c1 / c2​ ​

For option (d)

a1 / a2 = b1 / b2 = c1 / c2​ ​= -1 / 2

Test: Pair of Linear Equations in Two Variables (Medium) - Question 5
Save

Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Then the numbers are:
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 5
According to given information

Test: Pair of Linear Equations in Two Variables (Medium) - Question 6
Save

The solution of the equations x – y = 2 and x + y = 4 is:
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 6
Adding both equations, we have

Test: Pair of Linear Equations in Two Variables (Medium) - Question 7
Save

For which values of a and b, will the following pair of linear equations have infinitely many solutions?

x + 2y = 1

(a – b)x + (a + b)y = a + b – 2
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 7
For infinitely many solutions

Test: Pair of Linear Equations in Two Variables (Medium) - Question 8
Save

The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son’s age. The present ages, in years, of the son and the father are, respectively
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 8
Let the age of father be x and of son is y.

Then according to question,

x = 6y …..(i)

Four years hence age of son will be y + 4 and age of father will be x + 4

Then according to question,

x + 4 = 4 (y + 4)

x – 4y = 12 …..(ii)

Solving equations (i) and (ii) we get:

y = 6 and x = 36

Test: Pair of Linear Equations in Two Variables (Medium) - Question 9
Save

Rakshita has only Rs. 1 and Rs. 2 coins with her. If the total number of coins that she has is 50 and the amount of money with her is Rs 75, then the number of Rs.1 andRs.2 coins is, respectively
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 9
Let her number of Rs.1 coins are x

Let the number of Rs.2 coins are y

Then

By the given conditions x + y = 50 …..(i)

1 × x + 2 × y = 75 ⇒ x + 2y = 75 …..(ii)

Solving equations (i) and (ii) we get:

(x + 2y) – (x + y) = 75 – 50 ⇒ y = 25

Therefore, x = 50 – 25 = 25

So the number of coins are 25, 25 each.

Test: Pair of Linear Equations in Two Variables (Medium) - Question 10
Save

In a competitive examination, one mark is awarded for each correct answer while 1/2 mark is deducted for every wrong answer. Jayanti answered 120 questions and got 90 marks. How many questions did she answer correctly?
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 10
Let x be the number of correct answers of the questions in a competitive exam.

Then, 120 − x be the number of wrong answers

Then by given condition

Test: Pair of Linear Equations in Two Variables (Medium) - Question 11
Save

The angles of a cyclic quadrilateral ABCD are:

∠A = (6x + 10)0, ∠B = (5x)0

∠C = (x + y)0, ∠D = (3y - 10)0

Then value of x and y are:
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 11
In cyclic quadrilateral, sum of opposite angles is 1800

Therefore

6x + 10 + x + y = 180

⇒ 7x + y = 170 …..(i)

5x + 3y – 10 = 180

⇒ 5x + 3y = 190 …..(ii)

Multiplying equations (i) and (ii), we get:

x = 20o and y = 30o

Test: Pair of Linear Equations in Two Variables (Medium) - Question 12
Save

A shopkeeper gives books on rent for reading. She takes a fixed charge for the first two days, and an additional charge for each day thereafter. Reema paid Rs. 22 for a book kept for six days, while Ruchika paid Rs 16 for the book kept for four days, then the charge for each extra day is:
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 12
Let Rs. x be the fixed charge and Rs. y be the charge for each extra day.

Then by the given conditions

x + 4y = 22 …..(i)

x + 2y = 16 …..(ii)

Subtracting equation (ii) from (i), we get:

y = Rs. 3

Test: Pair of Linear Equations in Two Variables (Medium) - Question 13
Save

Aruna has only Re. 1 and Rs. 2 coins with her. If the total number of coins that she has is 50 and the amount of money with her is Rs. 75, then the number of Re. 1 and Rs. 2 coins are respectively
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 13
Let number of Re.1 coin = x

Number of Re. 2 coin = y

A / q,

x + y = 50 ..............................(i)

x + 2y = 75 ..............................(ii)

On Solving eqn. (i) and (ii), we get

x = 25 and y = 25

Test: Pair of Linear Equations in Two Variables (Medium) - Question 14
Save

The pair of equations x = a and y = b graphically represents lines which are
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 14
The equations are x = a and y = b.

The graph of x = a is a line parallel to y-axis and y = b is a line parallel to x-axis.

∴ The angle between them is 90o , i.e. they intersect.

So, the equations are consistent.

Now solving simultaneously, the solution is (a, b).

So, the point of intersection is (a, b).

Test: Pair of Linear Equations in Two Variables (Medium) - Question 15
Save

The value of k, for which equations 3x + 5y = 0 and kx + 10y = 0 has a non-zero solution is
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 15
For a system of equations a1x + b1y + c1 ​= 0; a2x + b2y + c2 = 0 to have non-zero solutions, the condition to be satisfied is

a1 / a2 = b1 / b2 = c1 / c2​ ​

∴ 3 / k = 5 / 10 ​

or k = 6

Test: Pair of Linear Equations in Two Variables (Medium) - Question 16
Save

Two equations in two variables taken together are called
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 16
Two linear equations in two variables taken together are called simultaneous linear equations. The solution of system of simultaneous linear equation is the ordered pair (x, y) which satisfies both the linear equations.
Test: Pair of Linear Equations in Two Variables (Medium) - Question 17
Save

The pairs of equations x + 2y - 5 = 0 and -4x - 8y + 20 = 0 have:
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 17
a1 / a2 = 1 / -4

b1 / b2 = 2 / -8 = 1 / -4

c1 / c2 = -5 / 20 = -1 / 4

This shows:

a1 / a2 = b1 / b2 = c1 / c2

Therefore, the pair of equations has infinitely many solutions.

Test: Pair of Linear Equations in Two Variables (Medium) - Question 18
Save

If a pair of linear equations is consistent, then the lines are:
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 18
Because the two lines definitely have a solution.
Test: Pair of Linear Equations in Two Variables (Medium) - Question 19
Save

The pairs of equations 9x + 3y + 12 = 0 and 18x + 6y + 26 = 0 have
Detailed Solution for Test: Pair of Linear Equations in Two Variables (Medium) - Question 19
Given, 9x + 3y + 12 = 0 and 18x + 6y + 26 = 0

a1 / a2 = 9 / 18 = 1 / 2

b1 / b2 = 3 / 6 = 1 / 2

c1 / c2 = 12 / 26 = 6 / 13

Since, a1 / a2 = b1 / b2 ≠ c1 / c2

So, the pairs of equations are parallel and the lines never intersect each other at any point, therefore there is no possible solution.

Information about Test: Pair of Linear Equations in Two Variables (Medium) Page
In this test you can find the Exam questions for Test: Pair of Linear Equations in Two Variables (Medium) solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Pair of Linear Equations in Two Variables (Medium), EduRev gives you an ample number of Online tests for practice

Top Courses for Class 10

Download as PDF

Top Courses for Class 10

Important Questions for Pair of Linear Equations in Two Variables (Medium)

Find all the important questions for Pair of Linear Equations in Two Variables (Medium) at EduRev.Get fully prepared for Pair of Linear Equations in Two Variables (Medium) with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Pair of Linear Equations in Two Variables (Medium) syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Pair of Linear Equations in Two Variables (Medium) resources.

Pair of Linear Equations in Two Variables (Medium) MCQs with Answers

Prepare for the Pair of Linear Equations in Two Variables (Medium) within the Class 10 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Pair of Linear Equations in Two Variables (Medium)

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Pair of Linear Equations in Two Variables (Medium) with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup