Test: CPU & I/O Scheduling- 4 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: CPU & I/O Scheduling- 4
A computer has six tape drives, with n processes competing for them. Each process may need two drives. What is the maximum value of n for the system to be deadlock free?
Each Process Pi, i= 1.......9 is coded as follows
repeat
P(mutex)
{Critical section}
V(mutex)
forever
The code for P10 is identical except it uses V(mutex) in place of P(mutex). What is the largest number of processes that can be inside the critical section at any moment?
repeat
P(mutex)
{Critical section}
V(mutex)
forever
The code for P10 is identical except it uses V(mutex) in place of P(mutex). What is the largest number of processes that can be inside the critical section at any moment?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A system shares 9 tape drives. The current allocation and maximum requirement of tape drives for 4 processes are shown below: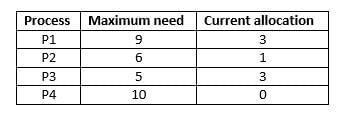
Which of the following best describes the current state of the system?
A solution to the Dining Philosophers Problem which avoids deadlock is:
Consider the following solution to the producer-consumer synchronization problem. The shared buffer size is N. Three semaphores empty, full and mutex are defined with respective initial values of 0, N and 1. Semaphore empty denotes the number of available slots in the buffer, for the consumer to read from. Semaphore full denotes the number of available slots in the buffer, for the producer to write to. The placeholder variables, denoted by P, Q, R and S, in the code below can be assigned either empty or full. The valid semaphore operations are: wait() and sigmal().

Which one of the following assignments to P, Q, R and S will yield the correct solution?
Consider a system with 3 processes that share 4 instances of the same resource type. Each process can request a maximum of K instances. Resource instances can be requested and released only one at a time. The largest value of K that will always avoid deadlock is _______ .
Note - This was Numerical Type question.
Which of the following is not true with respect to deadlock prevention and deadlock avoidance schemes ?
In a system, there are three types of resources: E, F and G. Four processes P0, P1, P2 and P3 execute concurrently. At the outset, the processes have declared their maximum resource requirements using a matrix named Max as given below. For example, Max[P2, F] is the maximum number of instances of F that P2 would require. The number of instances of the resources allocated to the various processes at any given state is given by a matrix named Allocation. Consider a state of the system with the Allocation matrix as shown below, and in which 3 instances of E and 3 instances of F are the only resources available.
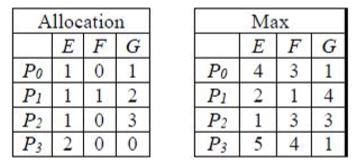
From the perspective of deadlock avoidance, which one of the following is true?
Which of the following is not true with respect to deadlock prevention and deadlock avoidance schemes?
Which of the following is not a necessary condition for deadlock?
What is the minimum number of resources required to ensure that deadlock will never occur, if there are currently three processes P1, P2 and P3 running in a system whose maximum demand for the resources of same type are 3, 4, and 5 respectively.
A total of 9 units of a resource type available, and given the safe state shown below, which of the following sequence will be a safe state?
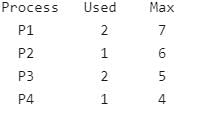
When a process is rolled back as a result of deadlock the difficulty which arises is
Consider a system having "n" resources of same type. These resources are shared by 3 processes, A, B, C. These have peak demands of 3, 4, and 6 respectively. For what value of "n" deadlock won't occur
In which of the following four necessary conditions for deadlock processes claim exclusive control of the resources they require?
Consider a system having m resources of the same type. These resources are shared by 3 processes A, B, C which have peak time demands of 3, 4, 6 respectively. The minimum value of m that ensures deadlock will never occur is
A counting semaphore was initialized to 10. Then 6 P (wait) operations and 4 V (signal) operations were completed on this semaphore. The resulting value of the semaphore is
A system has n resources R0,...,Rn-1,and k processes P0,....Pk-1.The implementation of the resource request logic of each process Pi is as follows:
if (i % 2 == 0) {
if (i < n) request Ri
if (i+2 < n) request Ri+2
}
else {
if (i < n) request Rn-i
if (i+2 < n) request Rn-i-2
}
In which one of the following situations is a deadlock possible?



















