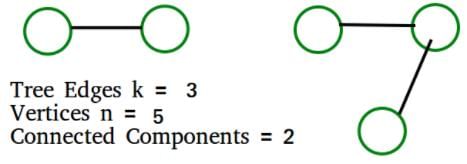Test: Graph - 2 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test - Test: Graph - 2
The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is
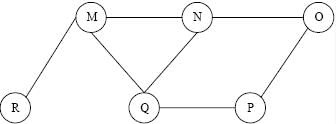

Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statements is always true?
Consider the following graph,

Among the following sequences:
(I) a b e g h f
(II) a b f e h g
(III) a b f h g e
(IV) a f g h b e
Which are depth first traversals of the above graph?

Among the following sequences:
(I) a b e g h f
(II) a b f e h g
(III) a b f h g e
(IV) a f g h b e
Which are depth first traversals of the above graph?
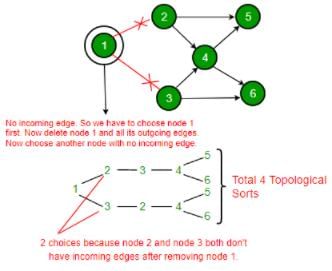
Consider the DAG with Consider V = {1, 2, 3, 4, 5, 6}, shown below. Which of the following is NOT a topological ordering?
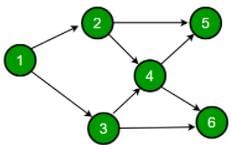
Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time on Depth First Search of G? Assume that the graph is represented using adjacency matrix.
Suppose depth first search is executed on the graph below starting at some unknown vertex. Assume that a recursive call to visit a vertex is made only after first checking that the vertex has not been visited earlier. Then the maximum possible recursion depth (including the initial call) is _________.
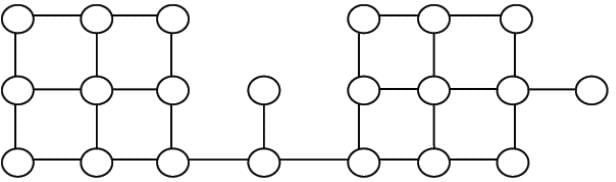
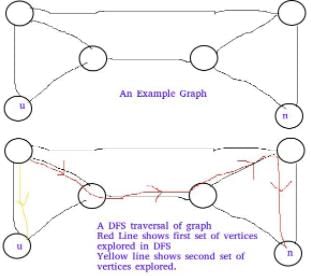
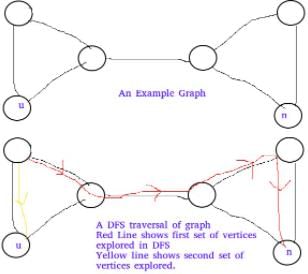
Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?
In a depth-first traversal of a graph G with n vertices, k edges are marked as tree edges. The number of connected components in G is
Consider the following directed graph.
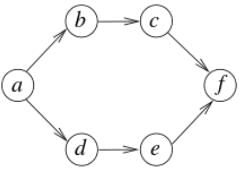
The number of different topological orderings of the vertices of the graph is
In an adjacency list representation of an undirected simple graph G = (V, E), each edge (u, v) has two adjacency list entries: [v] in the adjacency list of u, and [u] in the adjacency list of v. These are called twins of each other. A twin pointer is a pointer from an adjacency list entry to its twin. If |E| = m and |V | = n, and the memory size is not a constraint, what is the time complexity of the most efficient algorithm to set the twin pointer in each entry in each adjacency list?
Let G = (V, G) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighed edge (u, v) ∈ V×V is added to G. The worst case time complexity of determining if T is still an MST of the resultant graph is
Consider a complete binary tree with 7 nodes. Let A denote the set of first 3 elements obtained by performing Breadth-First Search (BFS) starting from the root. Let B denote the set of first 3 elements obtained by performing Depth-First Search (DFS) starting from the root.
The value of ∣A−B∣ is _______.
In a directed acyclic graph with a source vertex s, the quality-score of a directed path is defined to be the product of the weights of the edges on the path. Further, for a vertex v other than s, the quality-score of v is defined to be the maximum among the quality-scores of all the paths from s to v. The quality-score of s is assumed to be 1.
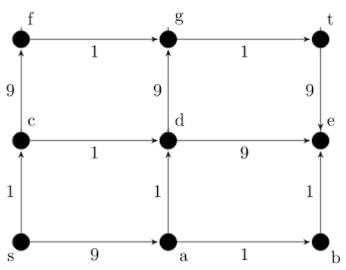
The sum of the quality-scores of all vertices on the graph shown above is _______ .
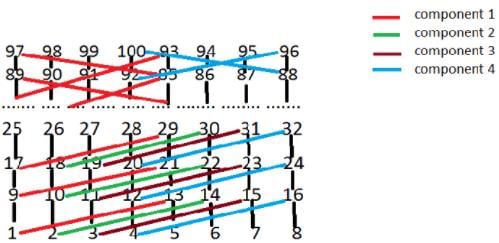
Let G be the graph with 100 vertices numbered 1 to 100. Two vertices i and j are adjacent iff |i−j|=8 or |i−j|=12. The number of connected components in G is
If we want to search any name in the phone directory , which is the most efficient data structure?
Consider a directed graph with n vertices and m edges such that all edges have same edge weights. Find the complexity of the best known algorithm to compute the minimum spanning tree of the graph?
What is the worst case efficiency for a path compression algorithm?
In an undirected connected planar graph G, there are eight vertices and five faces. The number of edges in G is _________.